题目内容
7.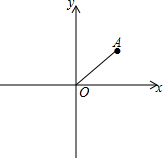 如图,在直角坐标系中,O是坐标原点,且点A坐标为(4,4),P是y轴上的一点,若以O,A,P三点组成的三角形为等腰三角形,求P点的坐标.
如图,在直角坐标系中,O是坐标原点,且点A坐标为(4,4),P是y轴上的一点,若以O,A,P三点组成的三角形为等腰三角形,求P点的坐标.
分析 由勾股定理得OA=4$\sqrt{2}$,(1)当OA为腰时,以O为圆心,OA为半径画弧交y轴于两点:(0,-4$\sqrt{2}$),(0,4$\sqrt{2}$);以A圆心,OA为半径画弧交y轴于一点(0,8);(2)当OA为底时,作线段OA的垂直平分线交y轴于点(0,4).
解答 解:由题可知OA=4$\sqrt{2}$,分两种情况进行讨论:
(1)当OA为腰时,以O为圆心,OA为半径画弧交y轴于两点,即(0,-4$\sqrt{2}$),(0,4$\sqrt{2}$);以A圆心,OA为半径画弧交y轴于一点,即(0,8).
(2)当OA为底时,作线段OA的垂直平分线交y轴于一点,即(0,4).
∴符合条件的点P有4个,坐标为(0,8)或(0,-4$\sqrt{2}$)或(0,4$\sqrt{2}$)或(0,4).
点评 本题考查了等腰三角形,围绕着线段OA为腰或底,分类讨论,运用圆规画弧法,形象易懂,充分运用等腰三角形的性质解题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
14.计算(-2x5)÷(-x3)÷($\frac{1}{3}$x)的结果是( )
| A. | $\frac{2}{3}$x | B. | -$\frac{2}{3}$x | C. | 6x | D. | -6x |
 如图,已知由x轴、一次函数y=kx+4(k<0)的图象及分别过点C(1,0)、D(4,0)两点作平行于y轴的两条直线所围成的图形ABDC的面积为7,试求这个一次函数的解析式.
如图,已知由x轴、一次函数y=kx+4(k<0)的图象及分别过点C(1,0)、D(4,0)两点作平行于y轴的两条直线所围成的图形ABDC的面积为7,试求这个一次函数的解析式.
 如图,点C是线段AB上一点,AC<AB,M,N分别是AB和CB的中点,AC=8,NB=5,求线段MN的长.
如图,点C是线段AB上一点,AC<AB,M,N分别是AB和CB的中点,AC=8,NB=5,求线段MN的长.