题目内容
9.把下列方程化成ax2+bx+c=0的形式,写出其中a,b,c的值,并计算b2-4ac的值:(1)x2-3x=4;
(2)4x2+1=4x;
(3)(2x+1)(x+2)=3.
分析 (1)运用移项法则把原方程变形,根据一元二次方程的定义解答即可;
(2)运用移项法则把原方程变形,根据一元二次方程的定义解答即可;
(3)运用整式的乘法法则把原方程变形,根据一元二次方程的定义解答即可.
解答 解:(1)x2-3x=4,
整理得,x2-3x-4=0,
a=1,b=-3,c=-4,
b2-4ac=(-3)2-4×1×(-4)=25;
(2)4x2+1=4x,
整理得,4x2-4x+1=0,
a=4,b=-4,c=1,
b2-4ac=(-4)2-4×1×4=0;
(3)(2x+1)(x+2)=3,
整理得,2x2+5x-1=0,
a=2,b=5,c=-1,
b2-4ac=52-4×5×(-1)=45.
点评 本题考查的是一元二次方程的一般形式是:ax2+bx+c=0(a,b,c是常数且a≠0),在一般形式中ax2叫二次项,bx叫一次项,c是常数项.其中a,b,c分别叫二次项系数,一次项系数,常数项.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.计算(-2x5)÷(-x3)÷($\frac{1}{3}$x)的结果是( )
| A. | $\frac{2}{3}$x | B. | -$\frac{2}{3}$x | C. | 6x | D. | -6x |
 如图,B、F、C、E在同一直线上,AC=DF,∠B=∠E,∠A=∠D,求证:BE=FC.
如图,B、F、C、E在同一直线上,AC=DF,∠B=∠E,∠A=∠D,求证:BE=FC.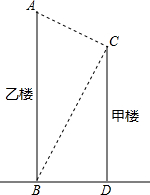 如图,在一幢高CD=15m的甲楼顶端C处,测得乙楼底部B的俯角为63°,乙楼顶端A的仰角为25°.求:
如图,在一幢高CD=15m的甲楼顶端C处,测得乙楼底部B的俯角为63°,乙楼顶端A的仰角为25°.求:
 如图,矩形ABCD的对角线AC,BD交于点O,E为CD的中点,延长OE至点F,使OE=EF.
如图,矩形ABCD的对角线AC,BD交于点O,E为CD的中点,延长OE至点F,使OE=EF.