题目内容
19.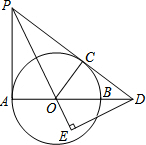 已知,如图,AB为⊙O的直径,PD切⊙O于点C,与AB的延长线交于点D,DE⊥PO交PO延长线于点E,连接PA,且∠EDB=∠EPA.
已知,如图,AB为⊙O的直径,PD切⊙O于点C,与AB的延长线交于点D,DE⊥PO交PO延长线于点E,连接PA,且∠EDB=∠EPA.(1)求证:PA是⊙O的切线;
(2)若PA=6,DA=8,求⊙O的半径.
分析 (1)欲证明PA是⊙O的切线,只需推知∠PAD=90°即可;通过相似三角形△APO~△EDO的对应角相等证得结论即可;
(2)在直角△PAD中,由PA与DA的长,利用勾股定理求出PD的长,由切线长定理得到PC=PA,由PD-PC求出CD的长,在直角△OCD中,设OC=r,则有OD=8-r,利用勾股定理列出关于r的方程,求出方程的解得到r的值,即为圆的半径.
解答  (1)证明:∵∠EDB=∠EPA,DE⊥PO,
(1)证明:∵∠EDB=∠EPA,DE⊥PO,
∴∠EDO=∠APO,∠DEO=90°.
又∵∠POA=∠DOE,
∴△APO~△EDO,
∴∠PAO=∠DEO=90°.
又∵OA是半径,
∴PA是⊙O的切线;
(2)解:在Rt△PAD中,若PA=6,DA=8,
根据勾股定理得:PD=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∵PD与PA都为圆的切线,
∴PC=PA=6,
∴DC=PD-PC=10-6=4,
在Rt△CDO中,设OC=r,则有DO=8-r,
根据勾股定理得:(8-r)2=r2+42,
解得:r=3,
则圆的半径为3.
点评 此题考查了切线的判定与性质,勾股定理,熟练掌握切线的判定与性质是解本题的关键.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
 设k≠0,若函数y1=(x-k)2+2k和y2=-(x+k)2-2k的图象与y轴依次交于A,B两点,函数y1,y2的图象的顶点分别为C,D.
设k≠0,若函数y1=(x-k)2+2k和y2=-(x+k)2-2k的图象与y轴依次交于A,B两点,函数y1,y2的图象的顶点分别为C,D.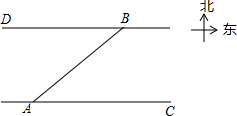 如图,一艘客轮以30km/h的速度由A码头出发沿北偏东53°方向航行至B码头,已知A、B两码头所在的河岸均为东西走向,河宽为16km,求该客轮至少用多长时间才能到达B码头?
如图,一艘客轮以30km/h的速度由A码头出发沿北偏东53°方向航行至B码头,已知A、B两码头所在的河岸均为东西走向,河宽为16km,求该客轮至少用多长时间才能到达B码头?
 用圆规、直尺作图,不写作法,但要保留作图痕迹.
用圆规、直尺作图,不写作法,但要保留作图痕迹. 解不等式组:$\left\{\begin{array}{l}{3(x-2)≤x-4}\\{\frac{1+2x}{3}>x-1}\end{array}\right.$并将其解集表示在如图所示的数轴上.
解不等式组:$\left\{\begin{array}{l}{3(x-2)≤x-4}\\{\frac{1+2x}{3}>x-1}\end{array}\right.$并将其解集表示在如图所示的数轴上.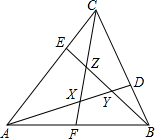 如图,△ABC中,D,E,F分别足BC,CA,AB边上的点,BD:DC=1:2,CE:EA=1:3,AF:FB=1:1,AD,BE,CF围成△XYZ,若△ABC的面积为1,求△XYZ的面积.
如图,△ABC中,D,E,F分别足BC,CA,AB边上的点,BD:DC=1:2,CE:EA=1:3,AF:FB=1:1,AD,BE,CF围成△XYZ,若△ABC的面积为1,求△XYZ的面积.