题目内容
9.有一列数a1,a2,a3,a4,…an,从第二个数开始,每一个数都等于1与它前面那个数的倒数差,如:a1=3,则a2=1-$\frac{1}{3}$=$\frac{2}{3}$,a3=1-$\frac{3}{2}$=-$\frac{1}{2}$…,请你计算当a1=2时,a2015的值是( )| A. | 2 | B. | $\frac{1}{2}$ | C. | -1 | D. | 2015 |
分析 根据这组数的运算规则找出该数列的前几项,能够发现a4=a1,从而得出该组数量每3项一循环的规律,结合2015÷3余2可得出结论.
解答 解:当a1=2时,a2=1-$\frac{1}{{a}_{1}}$=$\frac{1}{2}$,a3=1-$\frac{1}{{a}_{2}}$=-1,a4=1-$\frac{1}{{a}_{3}}$=2=a1,
由此发现,该数列每3个一循环,
∵2015÷3=671…2,
∴a2015=a2=$\frac{1}{2}$.
故选B.
点评 本题考查了数字的变化,解题的关键是列出数列的前几项找出“每3项一循环”的规律.本题属于中档题,难度不大,解决该题型题目时,找出数列前几项发现规律是关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
20.下列各情景分别可以用哪一幅图来近似的刻画?正确的顺序是( )
①汽车紧急刹车(速度与时间的关系)
②人的身高变化(身高与年龄的关系)
③跳高运动员跳跃横杆(高度与时间的关系)
④一面冉冉上升的红旗(高度与时间的关系)
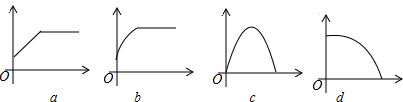
①汽车紧急刹车(速度与时间的关系)
②人的身高变化(身高与年龄的关系)
③跳高运动员跳跃横杆(高度与时间的关系)
④一面冉冉上升的红旗(高度与时间的关系)
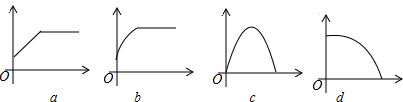
| A. | abcd | B. | dabc | C. | dbca | D. | cabd |
17.下列情境①~④分别可以用哪幅图来近似地刻画?正确的顺序是( )
①一杯越来越凉的水(水温与时间的关系);
②一面冉冉升起的旗子(高度与时间的关系);
③足球守门员大脚开出去的球(高度与时间的关系)
④匀速行驶的汽车(速度与时间的关系).
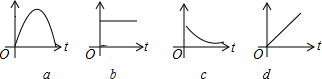
①一杯越来越凉的水(水温与时间的关系);
②一面冉冉升起的旗子(高度与时间的关系);
③足球守门员大脚开出去的球(高度与时间的关系)
④匀速行驶的汽车(速度与时间的关系).

| A. | cdab | B. | acbd | C. | dabc | D. | cbad |
18.已知一个菱形的周长是20cm,两条对角线的比是4:3,则这个菱形的面积是( )
| A. | 12cm2 | B. | 96cm2 | C. | 48cm2 | D. | 24cm2 |
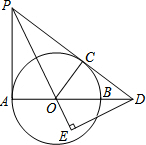 已知,如图,AB为⊙O的直径,PD切⊙O于点C,与AB的延长线交于点D,DE⊥PO交PO延长线于点E,连接PA,且∠EDB=∠EPA.
已知,如图,AB为⊙O的直径,PD切⊙O于点C,与AB的延长线交于点D,DE⊥PO交PO延长线于点E,连接PA,且∠EDB=∠EPA.
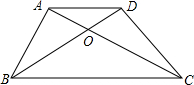 如图,梯形ABCD中,OD:OB=2:3,三角形AOB的面积是6平方厘米,求梯形ABCD的面积.
如图,梯形ABCD中,OD:OB=2:3,三角形AOB的面积是6平方厘米,求梯形ABCD的面积.