题目内容
10．
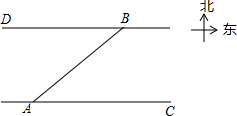如图，一艘客轮以30km/h的速度由A码头出发沿北偏东53°方向航行至B码头，已知A、B两码头所在的河岸均为东西走向，河宽为16km，求该客轮至少用多长时间才能到达B码头？（结果精确到0.1h，参考数据：sin53°≈$\frac{4}{5}$，cos53°≈$\frac{3}{5}$，tan53°≈$\frac{4}{3}$）
分析 首先过点A作AE⊥BD于点E，由题意可得：cos53°=$\frac{AE}{AB}$，进而得出AB的长即可得出答案．
解答 
解：如图所示：过点A作AE⊥BD于点E，
由题意可得：AE=16km，∠EAB=53°，
故cos53°=$\frac{AE}{AB}$=$\frac{16}{AB}$=$\frac{3}{5}$，
解得：AB=$\frac{80}{3}$，
∵客轮的速度为30km/h，
∴$\frac{80}{3}$÷30=$\frac{8}{9}$≈0.9（h），
答：该客轮至少用0.9h才能到达B码头．
点评 此题考查了方向角问题，注意结合实际问题，利用解直角三角形的相关知识求解是解此题的关键，注意数形结合思想的应用．
练习册系列答案
相关题目
1．下列命题中，
①三角形的外心是三角形三边垂直平分线的交点；
②函数y=（1-a）x2-4x+6与x轴只有一个交点，则a=$\frac{1}{3}$；
③半径分别为1和2的两圆相切，则圆心距为3；
④若对于任意x＞1的实数，都有ax＞1成立，则a≥1．
其中正确的个数有（ ）
①三角形的外心是三角形三边垂直平分线的交点；
②函数y=（1-a）x2-4x+6与x轴只有一个交点，则a=$\frac{1}{3}$；
③半径分别为1和2的两圆相切，则圆心距为3；
④若对于任意x＞1的实数，都有ax＞1成立，则a≥1．
其中正确的个数有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
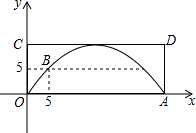如图，一座抛物线型拱桥，桥面CD与水面平行，在正常水位时桥下水面宽OA为30米，拱桥B处为警戒水位标识，点B到OC的水平距离和它到水面OA的距离都为5米．
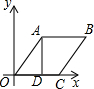请从以下两个小题中任选一个作答，若多选，则按所选的第一题计分．
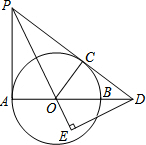已知，如图，AB为⊙O的直径，PD切⊙O于点C，与AB的延长线交于点D，DE⊥PO交PO延长线于点E，连接PA，且∠EDB=∠EPA．