题目内容
5.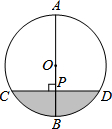 如图,AB为⊙O的直径,弦CD⊥AB于点P,CD=4$\sqrt{3}$,AP:PB=3:1.
如图,AB为⊙O的直径,弦CD⊥AB于点P,CD=4$\sqrt{3}$,AP:PB=3:1.(1)求⊙O的半径;
(2)求图中阴影部分的面积.
分析 (1)连接OC,OD,利用垂径定理得CP=2$\sqrt{3}$,AP=3x,PB=x,则AB=4x,OC=2x,OP=x,利用勾股定理可得结果;
(2)根据OP=2,OC=4,利用直角三角形的性质易得∠COD=120°,利用扇形和三角形的面积公式,求得阴影部分面积.
解答 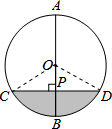 解:(1)连接OC,OD,
解:(1)连接OC,OD,
设AP=3x,PB=x,则AB=4x,OC=2x,OP=x,
∵CD⊥AB,
∴CP=DP=2$\sqrt{3}$,
∴x2+(2$\sqrt{3}$)2=(2x)2,
解得:x=2或x=-2(舍去),
∴OC=4,
∴⊙O的半径为4;
(2)∵OP=2,OC=4,
∴在Rt△OCP中,∠OCP=30°,∠COP=60°,
∴∠COD=120°,
∵S阴影=S扇形OCD-S△OCD
=$\frac{120°•π•{4}^{2}}{360°}$-$\frac{1}{2}$×4$\sqrt{3}$×2
=$\frac{16}{3}π-4\sqrt{3}$,
∴阴影部分的面积为:$\frac{16π}{3}-4\sqrt{3}$.
点评 本题主要考查了垂径定理,勾股定理,直角三角形的性质和扇形面积公式,作出适当的辅助线,数形结合是解答此题的关键.

练习册系列答案
相关题目
15.方程组$\left\{\begin{array}{l}{x+y=3}\\{3x-2y=4}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=0}\\{y=3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=3}\\{y=5}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ |
20.一元二次方程-x2+2x=-1的两个实数根为α,β,则α+β与α•β的值分别为( )
| A. | 2,-1 | B. | -2,-1 | C. | 2,1 | D. | -2,1 |
10.下列方程中有解的是( )
| A. | x2+x-1=0 | B. | x2+x+1=0 | C. | |x|=-1 | D. | $\frac{x-1}{x+2}$=$\frac{x-3}{2+x}$ |
14.计算a2•a4÷(-a2)2的结果是( )
| A. | a | B. | a2 | C. | -a2 | D. | a3 |
15.下列各式计算正确的是( )
| A. | (a2)3=a6 | B. | (π-1)0=0 | C. | a-1=-a(a≠0) | D. | (-2a)2=4a |