题目内容
17.有A、B、C三件商品,如果购买A商品3件、B商品2件、C商品1件共需315元;如果购买A商品1件、B商品2件、C商品3件共需285元,那么购买A、B、C各1件时共需150元.分析 设A、B和C商品的单价分别为x,y和z元,则根据“购买A商品3件,B商品2件,C商品1件,共需315元钱,购买A商品1件,B商品2件,C商品3件,共需285元钱”列出方程组,然后求解x+y+z即可.
解答 解:设A、B和C商品的单价分别为x,y和z元,
则根据题意得:$\left\{\begin{array}{l}{3x+2y+z=315①}\\{x+2y+3z=285②}\end{array}\right.$,
①+②式得:4x+4y+4z=600,
则x+y+z=150.
即购买A、B、C三种商品各1件时共需150元.
故答案为:150.
点评 本题考查三元一次方程的实际应用,解题关键是设出未知数,根据题意准确列出方程,此题不需要单独解出x、y和z,注意整体思想的灵活运用.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
8. 如图是一个圆锥的立体图形,则它的主视图为( )
如图是一个圆锥的立体图形,则它的主视图为( )
 如图是一个圆锥的立体图形,则它的主视图为( )
如图是一个圆锥的立体图形,则它的主视图为( )| A. |  | B. |  | C. |  | D. |  |
2.某班抽取6名同学参加体能测试,成绩如下:85,95,85,80,80,85.下列表述错误是( )
| A. | 众数是85 | B. | 平均数是85 | C. | 方差是20 | D. | 极差是15 |
6.下列运算正确的是( )
| A. | 3a2-a2=3 | B. | (a2)3=a5 | C. | a3•a6=a9 | D. | a(a-2)=a2-2 |
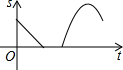
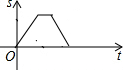
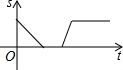
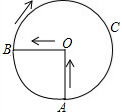 某景点有一座圆形的建筑,如图,小江从点A沿AO匀速直达建筑中心点O处,停留拍照后,从点O沿OB以同样的速度匀速走到点B,紧接着沿$\widehat{BCA}$回到点A,下面可以近似地刻画小江与中心点O的距离S随时间t变化的图象是( )
某景点有一座圆形的建筑,如图,小江从点A沿AO匀速直达建筑中心点O处,停留拍照后,从点O沿OB以同样的速度匀速走到点B,紧接着沿$\widehat{BCA}$回到点A,下面可以近似地刻画小江与中心点O的距离S随时间t变化的图象是( )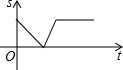
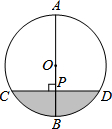 如图,AB为⊙O的直径,弦CD⊥AB于点P,CD=4$\sqrt{3}$,AP:PB=3:1.
如图,AB为⊙O的直径,弦CD⊥AB于点P,CD=4$\sqrt{3}$,AP:PB=3:1. 如图所示,点P是菱形ABCD对角线AC上的一点,连接DP并延长DP交边AB于点E,连接BP并延长BP交边AD于点F,交CD的延长线于点G.
如图所示,点P是菱形ABCD对角线AC上的一点,连接DP并延长DP交边AB于点E,连接BP并延长BP交边AD于点F,交CD的延长线于点G.