题目内容
16.某校将进行“校春季运动会”,现从全校学生中选出15名同学参加运动会相关服务工作,其中9名男生,6名女生.(1)若从这15名同学中随机选取1人作为联络员,求选到男生的概率.
(2)若运动会的某项服务工作只在A,B两位同学中选一人,准备用游戏的方式决定谁参加.游戏规则是:四个乒乓球上的数字分别为1,2,3,6(乒乓球只有数字不同,其余完全相同),将乒乓球放在不透明的纸箱中,从中任意摸取两个,若取到的两个乒乓球上的数字之和大于6则选A,否则选B,从是否公平的角度看,该游戏规则是否合理,用树状图或表格说明理由.
分析 (1)直接根据概率公式计算;
(2)先画出树状图,展示所有12种等可能的结果数,再找出两个数字之和大于6所占的结果数,计算出选A的概率和选B的概率,然后比较两概率大小判断该游戏规则是否合理.
解答 解:(1)选到男生的概率=$\frac{9}{15}$=$\frac{3}{5}$;
(2)画树状图: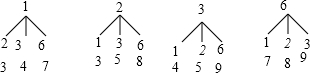
共有12种等可能的结果数,其中两个数字之和大于6占6种,所以选A的概率=$\frac{6}{12}$=$\frac{1}{2}$,
则选B的概率=1-$\frac{1}{2}$=$\frac{1}{2}$,
由于选甲的概率等于选乙的概率,
所以该游戏规则合理.
点评 本题考查了列表法与树状图法:利用列表法和树状图法展示所有可能的结果求出n,再从中选出符合事件A或B的结果数目m,求出概率.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
4.(-2)×$\frac{1}{2}$=( )
| A. | -2 | B. | 1 | C. | -1 | D. | $\frac{1}{2}$ |
1.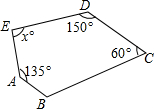 如图,若AB∥CD,则∠E的度数为( )
如图,若AB∥CD,则∠E的度数为( )
 如图,若AB∥CD,则∠E的度数为( )
如图,若AB∥CD,则∠E的度数为( )| A. | 60° | B. | 65° | C. | 70° | D. | 75° |
8. 如图是一个圆锥的立体图形,则它的主视图为( )
如图是一个圆锥的立体图形,则它的主视图为( )
 如图是一个圆锥的立体图形,则它的主视图为( )
如图是一个圆锥的立体图形,则它的主视图为( )| A. |  | B. |  | C. |  | D. |  |
6.下列运算正确的是( )
| A. | 3a2-a2=3 | B. | (a2)3=a5 | C. | a3•a6=a9 | D. | a(a-2)=a2-2 |
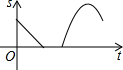
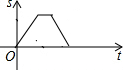
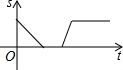
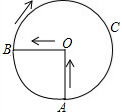 某景点有一座圆形的建筑,如图,小江从点A沿AO匀速直达建筑中心点O处,停留拍照后,从点O沿OB以同样的速度匀速走到点B,紧接着沿$\widehat{BCA}$回到点A,下面可以近似地刻画小江与中心点O的距离S随时间t变化的图象是( )
某景点有一座圆形的建筑,如图,小江从点A沿AO匀速直达建筑中心点O处,停留拍照后,从点O沿OB以同样的速度匀速走到点B,紧接着沿$\widehat{BCA}$回到点A,下面可以近似地刻画小江与中心点O的距离S随时间t变化的图象是( )
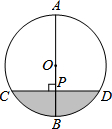 如图,AB为⊙O的直径,弦CD⊥AB于点P,CD=4$\sqrt{3}$,AP:PB=3:1.
如图,AB为⊙O的直径,弦CD⊥AB于点P,CD=4$\sqrt{3}$,AP:PB=3:1.