题目内容
 如图,反比例函数y=
如图,反比例函数y=| k |
| x |
| 2 |
考点:反比例函数图象上点的坐标特征,轴对称-最短路线问题
专题:
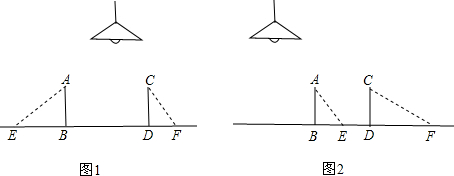
分析:延长AB交x轴于P,此时PA-PB值最大,最大值为AB,从而求得AB=2
,根据题意得出A(1,k),B(3,
),
然后根据勾股定理即可求得k的值.
| 2 |
| k |
| 3 |
然后根据勾股定理即可求得k的值.
解答:解:延长AB交x轴于P,此时PA-PB值最大,最大值为AB,
∵PA-PB的最大值为2
,
∴AB=2
,
∵反比例函数y=
(x>0)图象上的两点A、B的横坐标分别为1,3,
∴A(1,k),B(3,
),
∴AB=
=2
,解得k=3.
故答案为3.
∵PA-PB的最大值为2
| 2 |
∴AB=2
| 2 |
∵反比例函数y=
| k |
| x |
∴A(1,k),B(3,
| k |
| 3 |
∴AB=
(3-1)2+(
|
| 2 |
故答案为3.
点评:本题考查了反比例函数图象上点的坐标特征,轴对称-最短路线问题以及勾股定理的应用.

练习册系列答案
相关题目

 如图,直线AB,CD,EF相交于点O,EF⊥AB,OG为∠COF的平分线,若∠BOC:∠COG=5:1,求∠DOF的度数.
如图,直线AB,CD,EF相交于点O,EF⊥AB,OG为∠COF的平分线,若∠BOC:∠COG=5:1,求∠DOF的度数. 如图,AC,BD相交于点O,∠AOB=∠A,∠COD=∠D,试问:∠A与∠D之间的大小有什么关系?并说明理由.
如图,AC,BD相交于点O,∠AOB=∠A,∠COD=∠D,试问:∠A与∠D之间的大小有什么关系?并说明理由. 如图,点A,B在反比例函数y=-
如图,点A,B在反比例函数y=-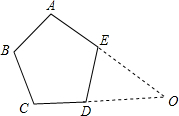 如图,已知正五边形ABCDE的边长为2.
如图,已知正五边形ABCDE的边长为2. 如图,OA=OB,OC=OD,∠O=50°,∠D=35°,则∠OBC等于
如图,OA=OB,OC=OD,∠O=50°,∠D=35°,则∠OBC等于