题目内容
 如图,点A,B在反比例函数y=-
如图,点A,B在反比例函数y=-| 4 |
| x |
考点:反比例函数图象上点的坐标特征
专题:
分析:作BE⊥x轴于E,AF⊥y轴于F,根据正方形的性质求得AB=BC=CD=DA,∠A=∠B=∠C=∠D=90°,进而求得∠BCE=∠CDO=∠DAF,从而求得△BEC≌△COD≌△DFA,得出BE=CO=DF,EC=OD=AF,从而求得B(2a,-a),代入反比例函数的解析式即可求得.
解答: 解:作BE⊥x轴于E,AF⊥y轴于F,
解:作BE⊥x轴于E,AF⊥y轴于F,
∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠A=∠B=∠C=∠D=90°,
∴∠BCE=∠CDO=∠DAF,
在△BEC和△COD和△DFA中,
,
∴△BEC≌△COD≌△DFA,
∴BE=CO=DF,EC=OD=AF,
∵点A,B的横坐标分别为a,2a(a<0),
∴EC=OD=AF=-a,EC+OC=-2a,
∴BE=CO=DF=-a,
∴B(2a,-a),
∵点B在反比例函数y=-
的图象上,
∴-a=-
,解得,a=-
.
 解:作BE⊥x轴于E,AF⊥y轴于F,
解:作BE⊥x轴于E,AF⊥y轴于F,∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠A=∠B=∠C=∠D=90°,
∴∠BCE=∠CDO=∠DAF,
在△BEC和△COD和△DFA中,
|
∴△BEC≌△COD≌△DFA,
∴BE=CO=DF,EC=OD=AF,
∵点A,B的横坐标分别为a,2a(a<0),
∴EC=OD=AF=-a,EC+OC=-2a,
∴BE=CO=DF=-a,
∴B(2a,-a),
∵点B在反比例函数y=-
| 4 |
| x |
∴-a=-
| 4 |
| 2a |
| 2 |
点评:本题考查了反比例函数图象上的点的坐标特征,待定系数法求解析式,作出辅助线构建全等三角形是解题的关键.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
在数轴上表示数a的点到原点的距离是4个长度,则a+|a|的值为( )
| A、0 | B、8 | C、0或8 | D、4 |
 如图,反比例函数y=
如图,反比例函数y= (1)小英从家向( )走到小红家,也可以向( )走到超市,( )走到小红家;
(1)小英从家向( )走到小红家,也可以向( )走到超市,( )走到小红家;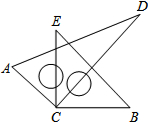 如图所示,将一副三角尺的直角顶点C叠放在一起,
如图所示,将一副三角尺的直角顶点C叠放在一起, 已知BD是平行四边形ABCD的对角线,过C点作CE∥BD,连接AE交BD的延长线于点F,请说明:AF=FE.
已知BD是平行四边形ABCD的对角线,过C点作CE∥BD,连接AE交BD的延长线于点F,请说明:AF=FE.