题目内容
如图1,△ABC中,∠C=90°,点O在AB上,⊙O经过点A,分别交于AC,AB于D,E,且∠1=∠A
(1)猜想:直线BD与⊙O的位置关系为 ,并证明你的猜想.
(2)如图2,当AD:AO=5:3,BC=20cm时,求BD的长.

(1)猜想:直线BD与⊙O的位置关系为
(2)如图2,当AD:AO=5:3,BC=20cm时,求BD的长.

考点:切线的判定
专题:计算题
分析:(1)连结OD,如图1,由互余得∠1+∠3=90°,而∠1=∠A,则∠A+∠3=90°,加上∠A=∠2,则∠2+∠3=90°,则根据切线的判定定理可得直线BD为⊙O的切线;
(2)如图2,连结DE,根据圆周角定理得∠ADE=90°,易证得Rt△ADE∽Rt△BCD,利用相似比得BD=
•BC,然后根据AD:AO=5:3和BC=20可计算出BD的长.
(2)如图2,连结DE,根据圆周角定理得∠ADE=90°,易证得Rt△ADE∽Rt△BCD,利用相似比得BD=
| AE |
| AD |
解答:解:(1)直线BD与⊙O相切.理由如下: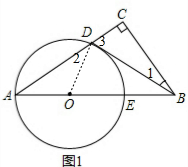
连结OD,如图1,
∵∠C=90°,
∴∠1+∠3=90°,
而∠1=∠A,
∴∠A+∠3=90°,
∵OA=OD,
∴∠A=∠2,
∴∠2+∠3=90°,即∠ODB=90°,
∴OD⊥BD,
∴直线BD为⊙O的切线.
故答案为相切;
(2)解:如图2,连结DE,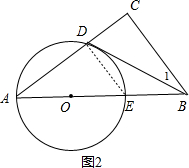
∵AE为直径,
∴∠ADE=90°,
∵∠1=∠A,
∴Rt△ADE∽Rt△BCD,
∴
=
,
∴BD=
•BC,
∵AD:AO=5:3,
∴AD:AE=5:6,
∴BD=
×20=24(cm).

连结OD,如图1,
∵∠C=90°,
∴∠1+∠3=90°,
而∠1=∠A,
∴∠A+∠3=90°,
∵OA=OD,
∴∠A=∠2,
∴∠2+∠3=90°,即∠ODB=90°,
∴OD⊥BD,
∴直线BD为⊙O的切线.
故答案为相切;
(2)解:如图2,连结DE,

∵AE为直径,
∴∠ADE=90°,
∵∠1=∠A,
∴Rt△ADE∽Rt△BCD,
∴
| AD |
| BC |
| AE |
| BD |
∴BD=
| AE |
| AD |
∵AD:AO=5:3,
∴AD:AE=5:6,
∴BD=
| 6 |
| 5 |
点评:本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了相似三角形的判定与性质.

练习册系列答案
相关题目
我市污水处理公司在环境污染整治行动中,添置了污水处理设备,每年排放的污水减少了135800吨,用科学记数法表示为(保留三个有效数字)( )
| A、135×103吨 |
| B、1.36×105吨 |
| C、1.35×105吨 |
| D、136×103吨 |
 如图所示,直线a,b,c两两相交,∠1=50°,∠2=
如图所示,直线a,b,c两两相交,∠1=50°,∠2= 如图,迎宾公园的喷水池边上有半圆形的石头(半径为1.12m)作为装饰,其中一块石头正前方5.88m处有一彩灯,某一时刻,该灯柱落在此半圆形石头上的影长为0.56πm.如果同一时刻,一直立0.6m的杆子的影长为1.8m,则灯柱的高
如图,迎宾公园的喷水池边上有半圆形的石头(半径为1.12m)作为装饰,其中一块石头正前方5.88m处有一彩灯,某一时刻,该灯柱落在此半圆形石头上的影长为0.56πm.如果同一时刻,一直立0.6m的杆子的影长为1.8m,则灯柱的高 如图,反比例函数y=
如图,反比例函数y=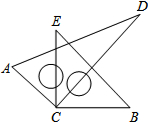 如图所示,将一副三角尺的直角顶点C叠放在一起,
如图所示,将一副三角尺的直角顶点C叠放在一起, 如图所示,∠AOB=90°,∠COD=90°,∠AOD=
如图所示,∠AOB=90°,∠COD=90°,∠AOD=