题目内容
 如图,OA=OB,OC=OD,∠O=50°,∠D=35°,则∠OBC等于
如图,OA=OB,OC=OD,∠O=50°,∠D=35°,则∠OBC等于考点:全等三角形的判定与性质
专题:
分析:利用“边角边”证明△OAD和△OBC全等,根据全等三角形对应角相等可得∠C=∠D,再利用三角形的内角和等于180°列式计算即可得解.
解答:解:在△OAD和△OBC中,
,
∴△OAD≌△OBC(SAS),
∴∠C=∠D=35°,
在△OBC中,∠OBC=180°-∠O-∠C=180°-50°-35°=95°.
故答案为:95°.
|
∴△OAD≌△OBC(SAS),
∴∠C=∠D=35°,
在△OBC中,∠OBC=180°-∠O-∠C=180°-50°-35°=95°.
故答案为:95°.
点评:本题考查了全等三角形的判定与性质,三角形的内角和定理,熟练掌握三角形全等的判定方法是解题的关键.

练习册系列答案
相关题目
 如图,反比例函数y=
如图,反比例函数y= 已知BD是平行四边形ABCD的对角线,过C点作CE∥BD,连接AE交BD的延长线于点F,请说明:AF=FE.
已知BD是平行四边形ABCD的对角线,过C点作CE∥BD,连接AE交BD的延长线于点F,请说明:AF=FE. 如图所示,∠AOB=90°,∠COD=90°,∠AOD=
如图所示,∠AOB=90°,∠COD=90°,∠AOD=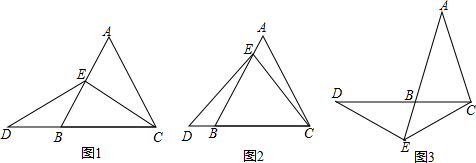
 如图所示,球体状容器的半径为R(R为常数),当液面高度为h时,水平液面面积A的函数表达式为
如图所示,球体状容器的半径为R(R为常数),当液面高度为h时,水平液面面积A的函数表达式为 如图所示,AC,BD是⊙O的两条直径,连接AD,BC,请你判断四边形ABCD的形状并说明道理.
如图所示,AC,BD是⊙O的两条直径,连接AD,BC,请你判断四边形ABCD的形状并说明道理.