题目内容
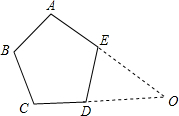 如图,已知正五边形ABCDE的边长为2.
如图,已知正五边形ABCDE的边长为2.(1)求正五边形ABCDE的一个内角的角度;
(2)如果AE和CD的延长线相交于点O,求DO的长.
考点:多边形内角与外角
专题:
分析:(1)首先求得正五边形ABCDE的内角和,即可求得每个内角的度数;
(2)作∠DEO的平分线,交DO于点F.根据角平分线、正五边形的性质,三角形内角和定理及外角的性质可得∠O=∠OEF=36°,∠DFE=∠ODE=72°,那么
OF=EF=DE=2,易证△DOF∽△DOE,根据相似三角形对应边成比例得出DF:DE=DE:OD,设DF=x,即x:2=2:(x+2),解方程即可.
(2)作∠DEO的平分线,交DO于点F.根据角平分线、正五边形的性质,三角形内角和定理及外角的性质可得∠O=∠OEF=36°,∠DFE=∠ODE=72°,那么
OF=EF=DE=2,易证△DOF∽△DOE,根据相似三角形对应边成比例得出DF:DE=DE:OD,设DF=x,即x:2=2:(x+2),解方程即可.
解答:解:(1)正五边形ABCDE的内角和是(5-2)×180=540°,
则正五边形ABCDE的一个内角=
=108°;
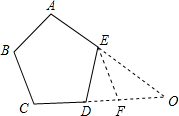 (2)作∠DEO的平分线,交DO于点F.
(2)作∠DEO的平分线,交DO于点F.
∵∠CDE=∠AED=108°,
∴∠ODE=∠OED=72°,
∴∠O=180°-∠ODE-∠OED=36°,∠DEF=∠OEF=
∠OED=36°,∠DFE=∠O+∠OEF=72°,
∴OF=EF=DE=2.
在△DEF与△DOE中,
∵∠EDF=∠ODE,∠DEF=∠O=36°,
∴△DEF∽△DOE,
∴DF:DE=DE:OD,
设DF=x,则DO=DF+FO=x+2.
则x:2=2:(x+2),
整理得,x2+2x-4=0,
解得x=
-1,
∴DO=
+1.
则正五边形ABCDE的一个内角=
| 540° |
| 5 |
 (2)作∠DEO的平分线,交DO于点F.
(2)作∠DEO的平分线,交DO于点F.∵∠CDE=∠AED=108°,
∴∠ODE=∠OED=72°,
∴∠O=180°-∠ODE-∠OED=36°,∠DEF=∠OEF=
| 1 |
| 2 |
∴OF=EF=DE=2.
在△DEF与△DOE中,
∵∠EDF=∠ODE,∠DEF=∠O=36°,
∴△DEF∽△DOE,
∴DF:DE=DE:OD,
设DF=x,则DO=DF+FO=x+2.
则x:2=2:(x+2),
整理得,x2+2x-4=0,
解得x=
| 5 |
∴DO=
| 5 |
点评:本题考查了多边形内角与外角,角平分线、正五边形的性质,三角形内角和定理,三角形外角的性质,相似三角形的判定与性质等知识,难度适中.准确作出辅助线是解决第(2)问的关键.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
在数轴上表示数a的点到原点的距离是4个长度,则a+|a|的值为( )
| A、0 | B、8 | C、0或8 | D、4 |
 如图,反比例函数y=
如图,反比例函数y=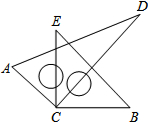 如图所示,将一副三角尺的直角顶点C叠放在一起,
如图所示,将一副三角尺的直角顶点C叠放在一起, 如图所示,在射线OF上,顺次取A,B,C,D四点,使AB:BC:CD=2:3:4,又m,n分别是AB,CD的中点.已知AD=90cm,求MN的长.
如图所示,在射线OF上,顺次取A,B,C,D四点,使AB:BC:CD=2:3:4,又m,n分别是AB,CD的中点.已知AD=90cm,求MN的长. 已知BD是平行四边形ABCD的对角线,过C点作CE∥BD,连接AE交BD的延长线于点F,请说明:AF=FE.
已知BD是平行四边形ABCD的对角线,过C点作CE∥BD,连接AE交BD的延长线于点F,请说明:AF=FE. 如图所示,∠AOB=90°,∠COD=90°,∠AOD=
如图所示,∠AOB=90°,∠COD=90°,∠AOD= 如图所示,AC,BD是⊙O的两条直径,连接AD,BC,请你判断四边形ABCD的形状并说明道理.
如图所示,AC,BD是⊙O的两条直径,连接AD,BC,请你判断四边形ABCD的形状并说明道理.