题目内容
11.下列图形中,既是中心对称图形又是轴对称图形的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据轴对称图形与中心对称图形的概念求解.
解答 解:第一个图形是轴对称图形,也是中心对称图形;
第二个图形是轴对称图形,不是中心对称图形;
第三个图形是轴对称图形,不是中心对称图形;
第四个图形是轴对称图形,也是中心对称图形.
故选B.
点评 本题考查了中心对称图形与轴对称图形的知识.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后两部分重合.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
1.为了解学生课外阅读的喜好,某校从六年级随机抽取部分学生进行问卷调查,调查要求每人只选取一种喜欢的书籍,如果没有喜欢的书籍,则作“其他”类统计,图(1)与图(2)是整理数据后绘制的两幅不完整的统计图,以下结论不正确的是( )


| A. | 由这两个统计图不能确定喜欢”小说”的人数 | |
| B. | 若该年级共有1200名学生,则可估计喜爱“科普常识”的学生有360人 | |
| C. | 由这两个统计图可知喜好“科普常识”的学生有90人 | |
| D. | 在扇形统计图中,“漫画”所在扇形的圆心角为72° |
1.在一个不透明的盒子里装有黑、白两种颜色的球共40只,这些球除颜色外其余完全相同.小颖做摸球实验,搅匀后,她从盒子里随机摸出一只球记下颜色后,再把球放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
(1)请估计:当n很大时,摸到白球的频率将会接近0.6;(精确到0.1)
(2)若从盒子里随机摸出一只球,则摸到白球的概率的估计值为0.6;
(3)试估算盒子里黑、白两种颜色的球各有多少只?
| 摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
| 摸到白球的次数m | 65 | 124 | 178 | 302 | 481 | 599 | 1803 |
| 摸到白球的频率$\frac{m}{n}$ | 0.65 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
(2)若从盒子里随机摸出一只球,则摸到白球的概率的估计值为0.6;
(3)试估算盒子里黑、白两种颜色的球各有多少只?
 如图,直线a,b被直线c所截,若a∥b,∠1=42°,则∠2=138度.
如图,直线a,b被直线c所截,若a∥b,∠1=42°,则∠2=138度.



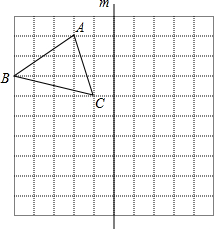 如图所示的正方形网格中,每个小正方形的边长均为1个单位,△ABC的三个顶点都在格点上.
如图所示的正方形网格中,每个小正方形的边长均为1个单位,△ABC的三个顶点都在格点上.