题目内容
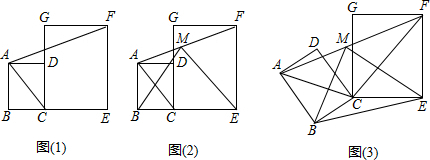
6.一个小球在如下几种图案地砖上自由滚动,小球停在阴影区域的概率最大的是( )| A. |  | B. |  | C. |  | D. |  |
分析 根据几何概率的计算方法分别求出各选项中小球停在阴影区域的概率,然后比较概率的大小即可得到答案.
解答 解:A、小球停在阴影区域的概率=$\frac{3}{9}$=$\frac{1}{3}$;
B、小球停在阴影区域的概率=$\frac{1}{2}$;
C、小球停在阴影区域的概率=$\frac{5}{9}$,
D、小球停在阴影区域的概率=$\frac{4}{9}$.
故选C.
点评 本题考查几何概率:首先根据题意将代数关系用面积表示出来,一般用阴影区域表示所求事件(A);然后计算阴影区域的面积在总面积中占的比例,这个比例即事件(A)发生的概率.

练习册系列答案
相关题目
1.我县某初中学校举办“经典诵读”比赛,13名学生进入决赛,他们所得分数互不相同,比赛共设7个获奖名额,某学生知道自己的分数后,要判断自己能否获奖,他应该关注的统计量是( )
| A. | 众数 | B. | 中位数 | C. | 平均数 | D. | 方差 |
11.下列图形中,既是中心对称图形又是轴对称图形的有( )

| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
16.下列各式计算正确的是( )
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 2$\sqrt{2}$-$\sqrt{2}$=$\sqrt{2}$ | C. | $\sqrt{(-4)×(-9)}$=$\sqrt{-4}$×$\sqrt{-9}$ | D. | $\sqrt{6}$÷$\sqrt{3}$=$\sqrt{3}$ |