题目内容
16．
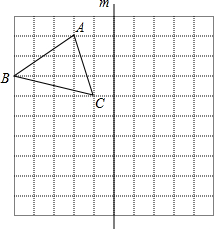如图所示的正方形网格中，每个小正方形的边长均为1个单位，△ABC的三个顶点都在格点上．（1）在网格中画出△ABC向下平移3个单位得到的△A1B1C1；
（2）在网格中画出△ABC关于直线m对称的△A2B2C2；
（3）在直线m上画一点P，使得|PA-PC2|的值最大．
分析 （1）根据图形平移的性质画出△A1B1C1即可；
（2）画出△ABC关于直线m对称的△A2B2C2即可；
（3）过点A2B2作直线，此直线与直线m的交点即为所求．
解答 
解：作图如下：
（1）如图，△A1B1C1．
（2）如图，△A2B2C2．
（3）如图，点P即为所求．
点评 本题考查的是作图-轴对称变换，熟知轴对称的性质是解答此题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
6．某校初三（2）班40名同学为“希望工程”捐款，共捐款100元，捐款情况如表：
表格中捐款2元和3元的人数不小心被墨水污染已经看不清楚．
若设捐款2元的有x名同学，捐款3元的有y名同学，根据题意，可得方程组（ ）
| 捐款（元） | 1 | 2 | 3 | 4 |
| 人数（人） | 6 | ● | ● | 7 |
若设捐款2元的有x名同学，捐款3元的有y名同学，根据题意，可得方程组（ ）
| A． | $\left\{\begin{array}{l}{x+y=27}\\{2x+3y=66}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x+y=27}\\{2x+3y=100}\end{array}\right.$ | ||
| C． | $\left\{\begin{array}{l}{x+y=27}\\{3x+2y=66}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x+y=27}\\{3x+2y=100}\end{array}\right.$ |
如图，△ABC是以BC为底边的等腰三角形，点A、C分别是一次函数$y=-\frac{3}{4}x+3$的图象与y轴、x轴的交点，点B在二次函数$y=\frac{1}{8}{x^2}+bx+c$的图象上，且该二次函数图象上存在一点D使四边形ABCD能构成平行四边形．
11．下列图形中，既是中心对称图形又是轴对称图形的有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
如图，水以恒速（即单位时间内注入水的体积相同）注入如图的容器中，容器中水的高度h与时间t的函数关系图象可能为（ ）
5．在直角坐标系中，将点P（-3，5）向右平移2个单位长度，再向上平移1个单位长度，可以得到对应点P1的坐标为（ ）
| A． | （-3，3） | B． | （-3，6） | C． | （-1，5） | D． | （-1，6） |