题目内容
已知cos72°=
,求cos36°.
| ||
| 4 |
考点:黄金分割
专题:
分析:由等腰△ABC中,AB=AC,∠BAC=36°,由cosC=cos72°=
,设BC=1,点D在边AC上且BD平分∠ABC,设CD=x.推出△ABC∽△BCD;由AD=BD=BC,根据AD+DC表示出AC,由两三角形相似得比例求出x的值即可;过B作BE垂直于AC,交AC于点E,在直角三角形ABE,利用锐角三角函数定义求出cos36°.
| ||
| 4 |
解答:解:∵等腰△ABC中,AB=AC,∠BAC=36°,
∴∠ABC=∠C=72°,
∵BD平分∠ABC,
∴∠ABD=∠CBD=36°,
∵∠CBD=∠A=36°,∠C=∠C,
∴△ABC∽△BCD;
∵∠A=∠ABD=36°,
∴AD=BD,
∵BD=BC,
∴AD=BD=BC=1,
设CD=x,则有AB=AC=x+1,
∵△ABC∽△BCD,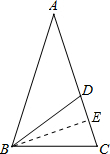
∴
=
,即
=
,
整理得:x2+x-1=0,
解得:x1=
,x2=
(负值,舍去),
过B作BE⊥AC,交AC于点E,
∵BD=BC,
∴E为CD中点,即DE=CE=
,
在Rt△ABE中,cosA=cos36°=
=
=
.
∴∠ABC=∠C=72°,
∵BD平分∠ABC,
∴∠ABD=∠CBD=36°,
∵∠CBD=∠A=36°,∠C=∠C,
∴△ABC∽△BCD;
∵∠A=∠ABD=36°,
∴AD=BD,
∵BD=BC,
∴AD=BD=BC=1,
设CD=x,则有AB=AC=x+1,
∵△ABC∽△BCD,

∴
| AB |
| BD |
| BC |
| CD |
| x+1 |
| 1 |
| 1 |
| x |
整理得:x2+x-1=0,
解得:x1=
| ||
| 2 |
-
| ||
| 2 |
过B作BE⊥AC,交AC于点E,
∵BD=BC,
∴E为CD中点,即DE=CE=
| ||
| 4 |
在Rt△ABE中,cosA=cos36°=
| AE |
| AB |
1+
| ||||
1+
|
| ||
| 4 |
点评:此题考查了相似三角形的判定与性质,锐角三角函数定义,以及一元二次方程的解法,熟练掌握相似三角形的判定与性质是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知sinA=0.1782,则锐角A的度数大约为( )
| A、8° | B、9° | C、10° |
 如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到点B′的位置,AB′与CD交于点E,且AB=8,AD=4.P为线段AC上的任意一点,PG⊥AE于G,PH⊥EC于H,则PG+PH的值为
如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到点B′的位置,AB′与CD交于点E,且AB=8,AD=4.P为线段AC上的任意一点,PG⊥AE于G,PH⊥EC于H,则PG+PH的值为 抛物线y=
抛物线y=