题目内容
画图说明如何将一条线段分为三等份？
考点：平行线分线段成比例
专题：作图题
分析：利用平行线分线段成比例定理：从线段AB的一个端点A引射线OM，再在射线AM上依次截取AE=EF=FG，然后连接GB，作FB∥GB交AB于D，作EC∥GB交AB于C点，则C点和D点为线段AB的三等份点．
解答：解：如图，
从线段AB的一个端点A引射线OM，
在射线AM上依次截取AE=EF=FG，
连接GB，过F点作FB∥GB交AB于D，过E点作EC∥GB交AB于C点，
则C点和D点为线段AB的三等份点．证明如下：
∵EC∥FD∥GB，
∴AE：EF：FD=AC：CD：DB，
而AE=EF=FG，
∴AC=CD=DB．
从线段AB的一个端点A引射线OM，在射线AM上依次截取AE=EF=FG，
连接GB，过F点作FB∥GB交AB于D，过E点作EC∥GB交AB于C点，
则C点和D点为线段AB的三等份点．证明如下：
∵EC∥FD∥GB，
∴AE：EF：FD=AC：CD：DB，
而AE=EF=FG，
∴AC=CD=DB．
点评：本题考查了平行线分线段成比例：三条平行线截两条直线，所得的对应线段成比例．
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
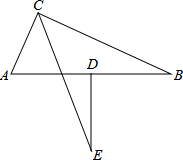在△ABC中，已知AB=13，BC=12，CA=5，D为边AB的中点，DE⊥AB且与∠ACB的平分线交于点E，求DE的长．
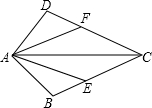已知，如图，AB=AD，CE=CF，AC是∠DAB的平分线，求证：AE=AF．