题目内容
 如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到点B′的位置,AB′与CD交于点E,且AB=8,AD=4.P为线段AC上的任意一点,PG⊥AE于G,PH⊥EC于H,则PG+PH的值为
如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到点B′的位置,AB′与CD交于点E,且AB=8,AD=4.P为线段AC上的任意一点,PG⊥AE于G,PH⊥EC于H,则PG+PH的值为考点:翻折变换(折叠问题)
专题:
分析:首先根据题意结合图形证明线段AE=CE,然后借助勾股定理求出AE的长度;借助三角形的面积公式即可解决问题.
解答: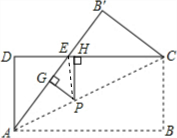 解:如图,连接EP;
解:如图,连接EP;
由翻折变换的性质可知:
∠EAC=∠BAC;
∵DC∥AB,
∴∠ECA=∠BAC,
∴∠EAC=∠ECA;
∴EA=EC(设为x),
∵DC=AB=8,
∴DE=8-x;
由勾股定理得:AE2=AD2+DE2,
即x2=(8-x)2+42,
解得:x=5;
∵S△AEC=
EC•AD=
×5×4,
S△AEC=S△APE+S△CPE,
而S△APE+S△CPE=
AE•PG+
EC•PH,
∴
×5×4=
×5×PG+
×5×PH,
∴PG+PH=4.
故该题答案为4.
 解:如图,连接EP;
解:如图,连接EP;由翻折变换的性质可知:
∠EAC=∠BAC;
∵DC∥AB,
∴∠ECA=∠BAC,
∴∠EAC=∠ECA;
∴EA=EC(设为x),
∵DC=AB=8,
∴DE=8-x;
由勾股定理得:AE2=AD2+DE2,
即x2=(8-x)2+42,
解得:x=5;
∵S△AEC=
| 1 |
| 2 |
| 1 |
| 2 |
S△AEC=S△APE+S△CPE,
而S△APE+S△CPE=
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴PG+PH=4.
故该题答案为4.
点评:该命题以矩形为载体,借助对称变换来考查全等三角形的性质、勾股定理、三角形的面积公式等几何知识;对分析问题、解决问题的能力提出了较高的要求.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
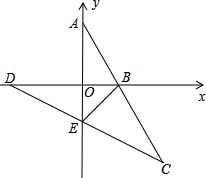 已知如图在平面直角坐标系中点A(0,2),点B(1,0),连接AB并延长至C,使BC=AB,点D(-4,0),DC与y轴交于点E,连接BE,试着判断∠AED与∠BEC的数量关系,并说明理由.
已知如图在平面直角坐标系中点A(0,2),点B(1,0),连接AB并延长至C,使BC=AB,点D(-4,0),DC与y轴交于点E,连接BE,试着判断∠AED与∠BEC的数量关系,并说明理由.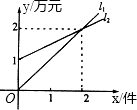 如图,l1表示某公司一种产品一天的销售收入与销售量的关系,l2表示该公司这种产品一天的销售成本与销售量的关系.
如图,l1表示某公司一种产品一天的销售收入与销售量的关系,l2表示该公司这种产品一天的销售成本与销售量的关系.