题目内容
15.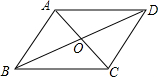 如图,四边形ABCD中,对角线AC、BD相交于点O,从下列条件:①AD∥BC,②AB=CD,③∠ABC=∠ADC,④OA=OC中任选两个.
如图,四边形ABCD中,对角线AC、BD相交于点O,从下列条件:①AD∥BC,②AB=CD,③∠ABC=∠ADC,④OA=OC中任选两个.(1)能证明四边形ABCD是平行四边形的有哪几种?请一一列举,并选择其中的一种加以证明;
(2)从不能证明四边形ABCD是平行四边形的选法中选择其中的一种举出反例(可用图形说明).
分析 (1)根据平行线的性质,可得∠ABC+∠BAD=180°,根据平行线的判定,可得AB与CD的关系,根据平行四边形的判定,可得答案;
(2)根据等腰梯形的判定,可得答案.
解答 解:(1)三种:①AD∥BC,③∠ABC=∠ADC;①AD∥BC,④OA=OC;②AB=CD,③∠ABC=∠ADC;
已知AD∥BC,③∠ABC=∠ADC,证明四边形ABCD是平行四边形.
证明:∵AD∥BC,
∴∠ABC+∠BAD=180°.
∵∠ABC=∠ADC,
∴∠BAD+∠ADC=180°,
∴AB∥CD,
又∵AD∥BC,
∴四边形ABCD是平行四边形;
(2)①AD∥BC,②AB=CD,四边形ABCD不是平行四边形,
如图: ,
,
四边形ABCD是等腰梯形.
点评 本题考查了平行四边形的判定,熟记平行四边形的判定与性质是解题关键.

练习册系列答案
 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
4.如果多边形的内角和是外角和的7倍,那么这个多边形的边数是( )
| A. | 7 | B. | 12 | C. | 14 | D. | 16 |
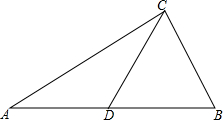 如图,在△ABC中,CD是边AB上的中线,AC=8,BC=6,CD=5,求证:△ABC是直角三角形.
如图,在△ABC中,CD是边AB上的中线,AC=8,BC=6,CD=5,求证:△ABC是直角三角形.