题目内容
8.计算:$\frac{1}{1-x}$+$\frac{1}{1+x}$+$\frac{2}{1+x^2}$+$\frac{4}{1+{x}^{4}}$+$\frac{-8}{1-{x}^{8}}$=0.分析 根据前两项结合,通分把异分母分式化为同分母分式,然后再相加减,可得答案.
解答 解:原式=$\frac{2}{1-{x}^{2}}$+$\frac{2}{1+x^2}$+$\frac{4}{1+{x}^{4}}$+$\frac{-8}{1-{x}^{8}}$
=$\frac{4}{1-{x}^{4}}$+$\frac{4}{1+{x}^{4}}$+$\frac{-8}{1-{x}^{8}}$
=$\frac{8}{1-{x}^{8}}$+$\frac{-8}{1-{x}^{8}}$=0,
故答案为:0.
点评 本题考查了分式的加减法,分式的加减运算中,如果是同分母分式,那么分母不变,把分子直接相加减即可;如果是异分母分式,则必须先通分,把异分母分式化为同分母分式,然后再相加减.

练习册系列答案
相关题目
18.对于实数c,d,我们可用min{c,d}表示c,d两数中较小的数,如min{3,-1}=-1.则关于x的代数式min{3x${\;}^{2}-\frac{3}{2}$,x2+2x+1}的最小值是( )
| A. | $\frac{3}{2}$ | B. | -1 | C. | -$\frac{3}{2}$ | D. | -2 |
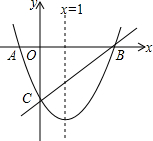 如图,对称轴为直线x=1的抛物线y=ax2+bx+c交x轴于A,B,交y轴的负半轴于C,A的坐标为(-1,0),OA=$\frac{1}{3}$OC.
如图,对称轴为直线x=1的抛物线y=ax2+bx+c交x轴于A,B,交y轴的负半轴于C,A的坐标为(-1,0),OA=$\frac{1}{3}$OC.