题目内容
18．对于实数c，d，我们可用min{c，d}表示c，d两数中较小的数，如min{3，-1}=-1．则关于x的代数式min{3x${\;}^{2}-\frac{3}{2}$，x2+2x+1}的最小值是（ ）| A． | $\frac{3}{2}$ | B． | -1 | C． | -$\frac{3}{2}$ | D． | -2 |
分析 先分别求出y=3x${\;}^{2}-\frac{3}{2}$与y=x2+2x+1的最小值，再根据min{ c，d }表示c、d两数中较小的数即可求出代数式的最小值．
解答 解：∵y=3x${\;}^{2}-\frac{3}{2}$的最小值=-$\frac{3}{2}$，
y=x2+2x+1的最小值=$\frac{4×1×1-{2}^{2}}{4×1}$=0，
∵-$\frac{3}{2}$＜0，
∴关于x的代数式min{3x${\;}^{2}-\frac{3}{2}$，x2+2x+1}的最小值是-$\frac{3}{2}$．
故选C．
点评 本题考查的是二次函数的最值，熟知二次函数的顶点坐标公式是解答此题的关键．
练习册系列答案
相关题目
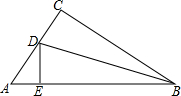如图，在△ABC中，AB=6cm，AC=3cm，BC=5cm，点D、E分别在AC、AB上，且△BCD和△BED关于BD对称，则△ADE的周长为4cm．
13．抛物线y=（x-1）2的顶点坐标是（ ）
| A． | （-1，0） | B． | （-1，1） | C． | （0，-1） | D． | （ 1，0） |
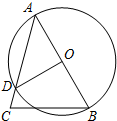如图，在△ABC中，AB是⊙O的直径，⊙O与AC交于点D，AC=$\sqrt{6}$，∠B=60°，∠C=75°．