��Ŀ����
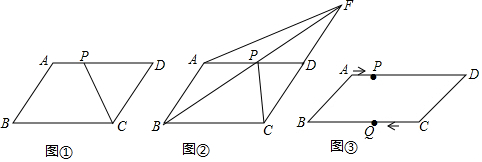
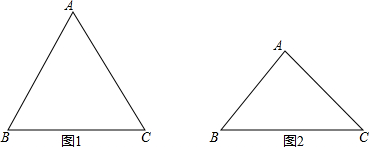
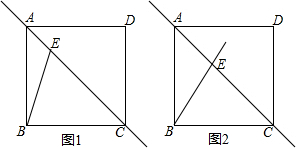
19����֪��ABC��AB=AC����BAC=������BA���ӳ�������ȡһ��D������D��BC��ƽ���߽�CA���ӳ����ڵ�E����1������BAC=60��ʱ����ͼ1�������ⲹȫͼ�Σ�ֱ��д��EC��BC��ED��������ϵ��
��2������BAC=90��ʱ����ͼ2���ж�EC��BC��ED֮���������ϵ��������֤����
��3������BAC=��ʱ��0�㣼����180�㣩����д��EC��BC��ED֮���������ϵ��д������˼·��
���� ��1��������֪��������ͼ�ɣ�
��2�����ۣ�BC+ED=$\sqrt{2}$BC��ֻҪ֤���ı���DECFΪƽ���ı��Σ���BDFΪ����ֱ�������Σ���Rt��BDF�У�BF2=BD2+DF2���Ƴ���BC+ED��2=2EC2���Ƴ�BC+ED=$\sqrt{2}$EC���ɣ�
��3�����ۣ�BC+ED=2EC•sin$\frac{��}{2}$���ɣ�2����֪�ı���ACFDΪƽ���ı��Σ���BDFΪ���������Σ���D����DN��BC��N��ɵ�BN=$\frac{1}{2}$BF����BDN=$\frac{1}{2}$������Rt��BDN��sin��BDN=$\frac{BN}{BD}$=sin$\frac{��}{2}$���ɵ�BC+ED=2EC•sin$\frac{��}{2}$��
��� �⣺��1��ͼ����ͼ��ʾ��
������ϵ��EC=BC+ED��
��2�����ۣ�BC+ED=$\sqrt{2}$BC��
���ɣ���D��DF��AC��BC�ӳ�����F�㣮
��DF��AC��ED��BC��
���ı���DECFΪƽ���ı��Σ�
��ED=CF��EC=DF��
��AB=AC��
���ABC=��ACB��
��ED��BC��
���DEC=��ECB����EDB=��DBC��
���CED=��BDE��
��AE=AD��
��EC=BD��
��BD=DF��
��DF��AC��
���BDF=��BAC=90�㣮
���BDFΪ����ֱ�������Σ�
��Rt��BDF��
��BF2=BD2+DF2��
�ࣨBC+ED��2=2EC2��
��BC+ED=$\sqrt{2}$EC��
��3�����ۣ�BC+ED=2EC•sin$\frac{��}{2}$��
���ɣ���ͼ��
�ɣ�2����֪�ı���ACFDΪƽ���ı��Σ���BDFΪ���������Σ�
��D����DN��BC��N��ɵ�BN=$\frac{1}{2}$BF����BDN=$\frac{1}{2}$����
��Rt��BDN��sin��BDN=$\frac{BN}{BD}$=sin$\frac{��}{2}$��
�ɵ�BC+ED=2EC•sin$\frac{��}{2}$��
���� ���⿼��ȱ������ε����ʡ�����ֱ�������ε����ʡ�ȫ�������ε��ж������ʵ�֪ʶ������Ĺؼ������������ѧ֪ʶ������⣬ѧ�����ӳ��ø����ߣ����������ı��ν�����⣬�����п��������ͣ�

 ���ݼ���ϵ�д�
���ݼ���ϵ�д�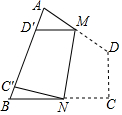 ��ͼ���ı���ֽƬABCD�У���A=75�㣬��B=65�㣬��ֽƬ�۵���ʹC��D����AB���ϵ�C�䣬D�䴦���ۺ�ΪMN�����AMD��+��BNC��=80�㣮
��ͼ���ı���ֽƬABCD�У���A=75�㣬��B=65�㣬��ֽƬ�۵���ʹC��D����AB���ϵ�C�䣬D�䴦���ۺ�ΪMN�����AMD��+��BNC��=80�㣮 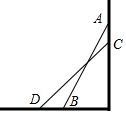 ��ͼ��һ����5�����ABб����һ��ֱ��ǽAO�ϣ���ʱAOΪ4�ף������͵Ķ���A��ǽ�»�1�ף���͵�B���Ƶľ���BD��������
��ͼ��һ����5�����ABб����һ��ֱ��ǽAO�ϣ���ʱAOΪ4�ף������͵Ķ���A��ǽ�»�1�ף���͵�B���Ƶľ���BD��������| A�� | ����1�� | B�� | ����1�� | C�� | С��1�� | D�� | ���϶����� |
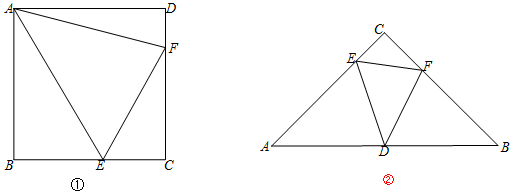
 ��ͼ��A��B��C�ǡ�O�ϵ����㣬����C=30�㣬OA=3����AB�ij�Ϊ�У�����������У�
��ͼ��A��B��C�ǡ�O�ϵ����㣬����C=30�㣬OA=3����AB�ij�Ϊ�У�����������У�