Question

11．解决问题时需要思考：是否解决过与其类似的问题．小明从问题1解题思路中获得启发从而解决了问题2．
问题1：如图①，在正方形ABCD中，E、F是BC、CD上两点，∠EAF=45°．

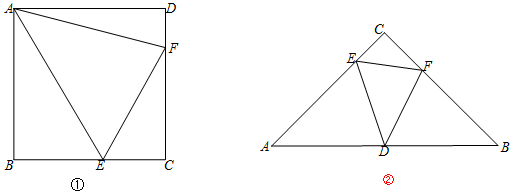
求证：∠AEF=∠AEB．
小明给出的思路为：延长EB到H，满足BH=DF，连接AH．请完善小明的证明过程．
问题2：如图②，在等腰直角△ABC中，∠ACB=90°，AC=BC=4，D为AB中点，E、F是AC、BC边上两点，∠EDF=45°．
（1）求点D到EF的距离．
（2）若AE=a，则S_△DEF=$\frac{{a}^{2}-4a+8}{a}$（用含字母a的代数式表示）．

Answer 1

分析 问题1：如图①中，延长EB到H，满足BH=DF，连接AH，只要证明△AHE≌△AFE，即可推出∠AEF=∠AEB；
问题2：（1）如图②中，过点D分别向AC、BC、EF作垂线，垂足分别为G、H、M，利用（1）中即可，根据角平分线的性质定理即可解决问题，
（2）在Rt△DEG中，DE=$\sqrt{E{G}^{2}+D{G}^{2}}$=$\sqrt{（a-2）^{2}+{2}^{2}}$=$\sqrt{{a}^{2}-4a+8}$，由S_△AED=$\frac{1}{2}$•AE•DG=a，△DEF∽△AED，推出$\frac{{S}_{△DEF}}{{S}_{△AED}}$=（$\frac{DE}{AE}$）²=$\frac{{a}^{2}-4a+8}{{a}^{2}}$，由此即可解决问题；

解答 问题1：证明：如图①中，延长EB到H，满足BH=DF，连接AH

∵AB=AD，∠ABH=∠D=90°，BH=DF，
∴△ADF≌ABH，
∴∠DAF=∠BAH，AF=AH，
∵∠DAF+∠BAE=∠BAD-∠EAF=90°-45°=45°，
即∠EAH=∠BAH+∠BAE=45°，
∴∠EAH=∠EAF，
又∵AF=AH，AE=AE，
∴△AHE≌△AFE，
∴∠AEF=∠AEB．

问题2：解：（1）过点D分别向AC、BC、EF作垂线，垂足分别为G、H、M，

∵∠ACB=90°，∴CGDH为矩形，∵AC=BC=4，D为AB中点，
∴DG=DH=$\frac{1}{2}$BC=2，
∴四边形CGDH为正方形，
由问题1知∠DEG=∠DEM，
∴DM=DG=2．

（2）在Rt△DEG中，DE=$\sqrt{E{G}^{2}+D{G}^{2}}$=$\sqrt{（a-2）^{2}+{2}^{2}}$=$\sqrt{{a}^{2}-4a+8}$，
∵S_△AED=$\frac{1}{2}$•AE•DG=a，
∵△DEF∽△AED，
∴$\frac{{S}_{△DEF}}{{S}_{△AED}}$=（$\frac{DE}{AE}$）²=$\frac{{a}^{2}-4a+8}{{a}^{2}}$，
∴S_△DEF=$\frac{{a}^{2}-4a+8}{a}$．
故答案为$\frac{{a}^{2}-4a+8}{a}$．

点评 本题考查正方形的性质、全等三角形的判定和性质、勾股定理相似三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考常考题型．