题目内容
8．
如图，在△ABC中，AD⊥BC于点D，若AC=3$\sqrt{2}$，∠C=45°，tan∠ABC=3，求BD的长．
分析 在Rt△ADC中利用三角函数求出AD的长，再根据tan∠ABC=3求出BD的长即可．
解答 解：在Rt△ADC中，AC=3$\sqrt{2}$，∠C=45°，
∵sinC=$\frac{AD}{AC}$，∴AD=ACsinC=3$\sqrt{2}$×$\frac{\sqrt{2}}{2}$=3
又∵在Rt△ABD中，tan∠ABC=3，
∴$\frac{AD}{BD}$=3，BD=1
即：BD的长为1
点评 本题考查了解直角三角形，解题的关键是掌握三角函数的概念及解直角三角形的方法．
练习册系列答案
浙江名校名师金卷系列答案
相关题目
16．秋季运动会即将召开，渝北校区将对校园进行彩旗装扮，计划把主干道一侧全部插上彩旗，要求路的两端各插一面，并且每两面旗帜的间隔相等．如果每隔4米插一面，则彩旗差23面；如果每隔5米插1面，则彩旗正好用完．设原有彩旗x面，主干道长为y米，则根据题意列出方程组正确的是（ ）
| A． | $\left\{\begin{array}{l}{\frac{y}{4}=x+23}\\{\frac{y}{5}+1=x}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{\frac{y}{4}+1=x+23}\\{\frac{y}{5}+1=x}\end{array}\right.$ | ||
| C． | $\left\{\begin{array}{l}{\frac{y}{4}+1=x+23}\\{\frac{y}{5}=x}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{\frac{y}{4}=x+23}\\{\frac{y}{5}=x}\end{array}\right.$ |
如图，在平面直角坐标系中，直线l1：y=kx+1交y轴于点A，交x轴于点B（3，0），直线l2平行于y轴，交直线l1于点D，交x轴于点E，E的坐标为（1，0），点P是直线l2上一动点（异于点D），连接PA、PB，设P（1，n）．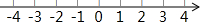
在数轴上画出表示下列各数的点，并回答下列问题：
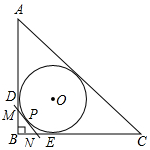如图，Rt△ABC的内切圆⊙O与两直角边AB，BC分别相切于点D、E，过劣弧（不包括端点D、E）上任一点P作⊙O的切线MN与AB、BC分别交于点M、N，若⊙O的半径为r．