题目内容
 如图⊙O中,AB是直径,弦GE⊥EF,HF⊥EF、GE、HF交AB于C、D,求证:AC=BD.
如图⊙O中,AB是直径,弦GE⊥EF,HF⊥EF、GE、HF交AB于C、D,求证:AC=BD.考点:垂径定理,梯形中位线定理
专题:证明题
分析:过点O作OM⊥EF于点M,由垂径定理可知EM=FM,再根据GE⊥EF,HF⊥EF可知CE∥OM∥DF,故OM是梯形CEFD的中位线,故OC=OD,再由OA=OB即可得出结论.
解答: 证明:过点O作OM⊥EF于点M,
证明:过点O作OM⊥EF于点M,
∵点O是圆心,
∴EM=FM.
∵GE⊥EF,HF⊥EF,
∴CE∥OM∥DF,
∴OM是梯形CEFD的中位线,
∴OC=OD.
∵OA=OB,
∴AC=BD.
 证明:过点O作OM⊥EF于点M,
证明:过点O作OM⊥EF于点M,∵点O是圆心,
∴EM=FM.
∵GE⊥EF,HF⊥EF,
∴CE∥OM∥DF,
∴OM是梯形CEFD的中位线,
∴OC=OD.
∵OA=OB,
∴AC=BD.
点评:本题考查的是垂径定理,熟知平分弦的直径平分这条弦,并且平分弦所对的两条弧是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
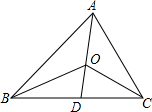 已知△ABC,三个内角的角平分线交于点O,∠OCB=30°,求∠BOD.
已知△ABC,三个内角的角平分线交于点O,∠OCB=30°,求∠BOD.