题目内容
10.一个口袋中有三个完全相同的小球,把它们分别标号为123,随机地摸出一个小球,然后放回,再随机摸出一个小球,则两次摸出的小球标号的和等于4的概率是$\frac{1}{3}$.分析 首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两次摸出的小球标号和为4的情况,再利用概率公式即可求得答案.
解答 解:根据题意,画树状图如下:
共有9种等可能结果,其中两次摸出的小球标号的和为4的有3种,
∴两次摸出的小球标号的和等于4的概率是$\frac{3}{9}$=$\frac{1}{3}$,
故答案为:$\frac{1}{3}$.
点评 此题考查了树状图法与列表法求概率.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
20. 如图,四边形ABCD是菱形,E、F、G、H分别是各边的中点,随机向菱形ABCD内部掷一粒米,则米粒落到阴影区域内的概率是( )
如图,四边形ABCD是菱形,E、F、G、H分别是各边的中点,随机向菱形ABCD内部掷一粒米,则米粒落到阴影区域内的概率是( )
 如图,四边形ABCD是菱形,E、F、G、H分别是各边的中点,随机向菱形ABCD内部掷一粒米,则米粒落到阴影区域内的概率是( )
如图,四边形ABCD是菱形,E、F、G、H分别是各边的中点,随机向菱形ABCD内部掷一粒米,则米粒落到阴影区域内的概率是( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{8}$ | D. | $\frac{2}{3}$ |
1.某校甲、乙、丙、丁四名同学在运动会上参加4×100米接力比赛,其中甲跑第一棒,那么乙跑第二棒的概率为( )
| A. | $\frac{1}{24}$ | B. | $\frac{1}{12}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{3}$ |
15. 如图,在等腰△ABC中,AB=AC,点D在AC边上,点E在BC边上,且∠AED=∠B,若AB=10,BE=5,AE=2$\sqrt{15}$,则线段CE的长为( )
如图,在等腰△ABC中,AB=AC,点D在AC边上,点E在BC边上,且∠AED=∠B,若AB=10,BE=5,AE=2$\sqrt{15}$,则线段CE的长为( )
 如图,在等腰△ABC中,AB=AC,点D在AC边上,点E在BC边上,且∠AED=∠B,若AB=10,BE=5,AE=2$\sqrt{15}$,则线段CE的长为( )
如图,在等腰△ABC中,AB=AC,点D在AC边上,点E在BC边上,且∠AED=∠B,若AB=10,BE=5,AE=2$\sqrt{15}$,则线段CE的长为( )| A. | $\frac{3\sqrt{15}}{2}$ | B. | 8 | C. | 2$\sqrt{15}$ | D. | 9 |
7.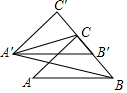 把△ABC沿BC方向平移,得到△A′B′C′,随着平移距离的不断增大,△A′CB的面积大小变化情况是( )
把△ABC沿BC方向平移,得到△A′B′C′,随着平移距离的不断增大,△A′CB的面积大小变化情况是( )
 把△ABC沿BC方向平移,得到△A′B′C′,随着平移距离的不断增大,△A′CB的面积大小变化情况是( )
把△ABC沿BC方向平移,得到△A′B′C′,随着平移距离的不断增大,△A′CB的面积大小变化情况是( )| A. | 增大 | B. | 减小 | C. | 不变 | D. | 不确定 |

 如图,在矩形ABCD中,点E、F分别在边AB、BC上,且AE=$\frac{1}{3}$AB=2,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,下列结论:①EF=2BE;②△APE≌△QEB;③FQ=3EQ;④SBFPE=8$\sqrt{3}$,其中正确的结论是①②③(只填序号).
如图,在矩形ABCD中,点E、F分别在边AB、BC上,且AE=$\frac{1}{3}$AB=2,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,下列结论:①EF=2BE;②△APE≌△QEB;③FQ=3EQ;④SBFPE=8$\sqrt{3}$,其中正确的结论是①②③(只填序号).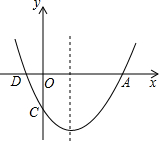 如图,二次函数y=ax2+bx+c的图象与x轴的交点为A、D(A在D的右侧),与y轴的交点为C,且A(4,0),C(0,-3),对称轴是直线x=1.
如图,二次函数y=ax2+bx+c的图象与x轴的交点为A、D(A在D的右侧),与y轴的交点为C,且A(4,0),C(0,-3),对称轴是直线x=1. 如图所示,图中是某中学初一(1)班某次期中考试成绩各个分数段人数的统计图,已知其中不及格同学的人数占全班人数的$\frac{1}{13}$.
如图所示,图中是某中学初一(1)班某次期中考试成绩各个分数段人数的统计图,已知其中不及格同学的人数占全班人数的$\frac{1}{13}$.