题目内容
15. 如图,在等腰△ABC中,AB=AC,点D在AC边上,点E在BC边上,且∠AED=∠B,若AB=10,BE=5,AE=2$\sqrt{15}$,则线段CE的长为( )
如图,在等腰△ABC中,AB=AC,点D在AC边上,点E在BC边上,且∠AED=∠B,若AB=10,BE=5,AE=2$\sqrt{15}$,则线段CE的长为( )| A. | $\frac{3\sqrt{15}}{2}$ | B. | 8 | C. | 2$\sqrt{15}$ | D. | 9 |
分析 根据等腰三角形的性质得到∠B=∠C,等量代换得到∠AED=∠C,根据相似三角形的性质得到$\frac{AE}{AD}=\frac{AC}{AE}$,求得AD=6,CD=4,然后根据相似三角形的性质即可得到结论.
解答 解: ∵AB=AC,
∵AB=AC,
∴∠B=∠C,
∵∠AED=∠B,
∴∠AED=∠C,
∵∠EAD=∠CAE,
∴△ACE∽△AED,
∴$\frac{AE}{AD}=\frac{AC}{AE}$,即$\frac{2\sqrt{15}}{AD}=\frac{10}{2\sqrt{15}}$,
∴AD=6,
∴CD=4,
∵∠B=∠C=∠AED,
∴∠BAE=180°-∠B-∠AEB,∠DEC=180°-∠AEB-∠AED,
∴∠BAE=∠DEC,
∴△ABE∽△ECD,
∴$\frac{AB}{BE}=\frac{CE}{CD}$,即$\frac{10}{5}$=$\frac{CE}{4}$,
∴CE=8.
故选B.
点评 本题考查了相似三角形的判定和性质,等腰三角形的性质,正确的识别图形是解题的关键.

练习册系列答案
相关题目
11.泰州火车站已于2016年5月15日正式开通动车,这极大地方便了我市市民的出行,根据以下信息,求出表中两列火车到达南京站的时间.
信息1:D5508和K722时刻表
信息2:泰州到南京铁路总长约为162千米.
信息3:K722在路上所用时间比D5508在路上所用时间多20%.
信息4:D5508的平均速度比K722的平均速度快18千米/时.
信息1:D5508和K722时刻表
| 车次 | 出发站 | 到达站 | 出发时间 | 到达时间 |
| D5508 | 泰州 | 南京 | 08:53 | |
| K722 | 泰州 | 南京 | 20:04 |
信息3:K722在路上所用时间比D5508在路上所用时间多20%.
信息4:D5508的平均速度比K722的平均速度快18千米/时.
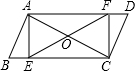 如图,已知?ABCD中,E,F分别在边BC,AD上,且BE=DF,AC,EF相交于O,连接AE,CF.
如图,已知?ABCD中,E,F分别在边BC,AD上,且BE=DF,AC,EF相交于O,连接AE,CF.