��Ŀ����
2��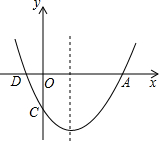 ��ͼ�����κ���y=ax2+bx+c��ͼ����x��Ľ���ΪA��D��A��D���Ҳࣩ����y��Ľ���ΪC����A��4��0����C��0��-3�����Գ�����ֱ��x=1��
��ͼ�����κ���y=ax2+bx+c��ͼ����x��Ľ���ΪA��D��A��D���Ҳࣩ����y��Ľ���ΪC����A��4��0����C��0��-3�����Գ�����ֱ��x=1����1������κ����Ľ���ʽ��
��2����M�ǵ���������������һ���㣬�Һ�����Ϊm�����ı���OCMA�����Ϊs����д��s��m֮��ĺ�����ϵʽ���������mΪ��ֵʱ���ı���OCMA��������
��3�����B��x���ϵĵ㣬P���������ϵĵ㣬�Ƿ���ڵ�P��ʹ����A��B��C��P�ĵ�Ϊ������ı���Ϊƽ���ı��Σ������ڣ�ֱ��д����P�����ꣻ�������ڣ���˵�����ɣ�
���� ��1�����������ߵĶԳ��Կɵõ���D���ܱ���Ȼ��A��C��D��������������ߵĽ���ʽ�����a��b��c��ֵ���Ӷ��ɵõ����κ����Ľ���ʽ��
��2����M��m��$\frac{3}{8}$x2-$\frac{3}{4}$x-3����|yM|=-$\frac{3}{8}$m2+$\frac{3}{4}$m+3����S=S��ACM+S��OAM�ɵõ�S��m�ĺ�����ϵʽ��Ȼ�������䷽�������S�����ֵ��
��3����ABΪƽ���ı��εı�ʱ����AB��PC�����P��������Ϊ-3����y=-3���������ߵĽ���ʽ����õ�P�ĺ����ꣻ��ABΪ�Խ���ʱ��AB��CP����ƽ�֣����P��������Ϊ3����y=3���������ߵĽ���ʽ����õ�P�ĺ����꣮
��� �⣺��1����A��4��0�����Գ�����ֱ��x=l��
��D��-2��0����
�֡�C��0��-3��
��$\left\{\begin{array}{l}{c=-3}\\{16a+4b+c=0}\\{4a-2b+c=0}\end{array}\right.$
��ã�a=$\frac{3}{8}$��b=-$\frac{3}{4}$��c=-3��
����κ�������ʽΪ��y=$\frac{3}{8}$x2-$\frac{3}{4}$x-3��
��2����ͼ1��ʾ��
��M��m��$\frac{3}{8}$x2-$\frac{3}{4}$x-3����|yM|=-$\frac{3}{8}$m2+$\frac{3}{4}$m+3��
��S=S��ACM+S��OAM
��S=$\frac{1}{2}$��OC��m+$\frac{1}{2}$��OA��|yM|=$\frac{1}{2}$��3��m+$\frac{1}{2}$��4����-$\frac{3}{8}$m2+$\frac{3}{4}$m+3��=-$\frac{3}{4}$m2+3m+6=-$\frac{3}{4}$��m-2��2+9��
��m=2ʱ��s�����9��
��3����ABΪƽ���ı��εı�ʱ����AB��PC��
��PC��x�ᣮ
���P��������Ϊ-3��
��y=-3����ã�$\frac{3}{8}$x2-$\frac{3}{4}$x-3=-3����ã�x=0��x=2��
���P��������2��-3����
��ABΪ�Խ���ʱ��
��ABCPΪƽ���ı��Σ�
��AB��CP����ƽ�֣�
���P��������Ϊ3��
��y=3����ã�$\frac{3}{8}$x2-$\frac{3}{4}$x-3=3�������ã�x2-2x-16=0����ã�x=1+$\sqrt{17}$��x=1-$\sqrt{17}$��
�������������ڵ�P��2��-3����P��1+$\sqrt{17}$��3����P��1-$\sqrt{17}$��3��ʹ����A��B��C��P�ĵ�Ϊ������ı���Ϊƽ���ı��Σ�
���� ������Ҫ������Ƕ��κ������ۺ�Ӧ�ã��������ҪӦ���˴���ϵ��������κ����Ľ���ʽ���䷽������κ�������ֵ��ƽ���ı��ε����ʣ�����ƽ���ı��ε����ʵõ���P���������ǽ���Ĺؼ���

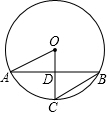 ��ͼ����O�İ뾶OC��ֱ����AB������ΪD��OA=2$\sqrt{2}$����B=22.5�㣬AB�ij�Ϊ��������
��ͼ����O�İ뾶OC��ֱ����AB������ΪD��OA=2$\sqrt{2}$����B=22.5�㣬AB�ij�Ϊ��������| A�� | 2 | B�� | 4 | C�� | 2$\sqrt{2}$ | D�� | 4$\sqrt{2}$ |
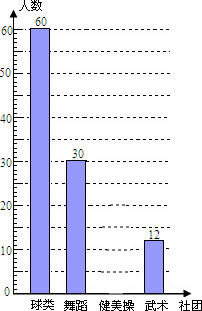 Ϊ�ƽ���ȫ������ѧ�����������˶�����ʵʩ����֯���ͬѧ��չ�������ϵĵڶ����û������ij��ѧ���齨�������ţ�����������ë��ƹ�����赸���š����������š��������ţ�Ϊ�˽���Уѧ������4�����Ż��ϲ���������У�����ȡ���ֳ����������ˡ�����ϲ���ĸ����š����飬����������ݻ��Ƴ����²�������ͳ�Ʊ��������ͼ���е���Ϣ����������⣺
Ϊ�ƽ���ȫ������ѧ�����������˶�����ʵʩ����֯���ͬѧ��չ�������ϵĵڶ����û������ij��ѧ���齨�������ţ�����������ë��ƹ�����赸���š����������š��������ţ�Ϊ�˽���Уѧ������4�����Ż��ϲ���������У�����ȡ���ֳ����������ˡ�����ϲ���ĸ����š����飬����������ݻ��Ƴ����²�������ͳ�Ʊ��������ͼ���е���Ϣ����������⣺| ������� | ���� | ռ���������� |
| ���� | 60 | m |
| �赸 | 30 | 0.25 |
| ������ | n | 0.15 |
| ���� | 12 | 0.1 |
��2���벹ȫͳ��ͼ��
��3���������60��ϲ������ͬѧ����3����ϲ����������У��3000��ѧ��������Ƹ�У��ϲ�������������
 �����Ŀ�ͨ����N��������д����˼���ķ��㣬��Ԫ�����ڼ䣬�ס�������Ӧ����A�е������ݲμ��ݳ����׳�˽�ҳ���N�г���1Сʱ���ҳ���������N�г������ȵ�A�л�վ��Ȼ����ת�˳����A�е������ݣ�����ʱ����Բ��ƣ�������ǡ��ͬʱ����A�е������ݣ������뿪N�еľ���y��ǧ�ף���˳�ʱ��x��Сʱ���Ĺ�ϵ��ͼ��ʾ������ͼ�����������⣺
�����Ŀ�ͨ����N��������д����˼���ķ��㣬��Ԫ�����ڼ䣬�ס�������Ӧ����A�е������ݲμ��ݳ����׳�˽�ҳ���N�г���1Сʱ���ҳ���������N�г������ȵ�A�л�վ��Ȼ����ת�˳����A�е������ݣ�����ʱ����Բ��ƣ�������ǡ��ͬʱ����A�е������ݣ������뿪N�еľ���y��ǧ�ף���˳�ʱ��x��Сʱ���Ĺ�ϵ��ͼ��ʾ������ͼ�����������⣺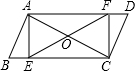 ��ͼ����֪?ABCD�У�E��F�ֱ��ڱ�BC��AD�ϣ���BE=DF��AC��EF�ཻ��O������AE��CF��
��ͼ����֪?ABCD�У�E��F�ֱ��ڱ�BC��AD�ϣ���BE=DF��AC��EF�ཻ��O������AE��CF��