题目内容
14.已知,⊙O的半径为R,AB和CD为⊙O的弦,且AB=$\sqrt{2}$R,弦CD=$\sqrt{3}$R,M、N分别是AB、CD的中点,则线段MN的最大值为$\frac{\sqrt{2}}{2}$R+$\frac{1}{2}$R,最小值为$\frac{\sqrt{2}}{2}$R-$\frac{1}{2}$R.分析 连接OA、OC,根据题意和垂径定理得到AM=$\frac{1}{2}$AB=$\frac{\sqrt{2}}{2}$R,CN=$\frac{1}{2}$CD=$\frac{\sqrt{3}}{2}$R,OM⊥AB,ON⊥CD,根据勾股定理求出OM、ON的长,计算即可.
解答 解: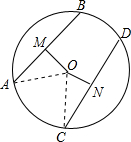 连接OA、OC,
连接OA、OC,
∵M、N分别是AB、CD的中点,
∴AM=$\frac{1}{2}$AB=$\frac{\sqrt{2}}{2}$R,CN=$\frac{1}{2}$CD=$\frac{\sqrt{3}}{2}$R,OM⊥AB,ON⊥CD,
∴OM=$\sqrt{O{A}^{2}-A{M}^{2}}$=$\frac{\sqrt{2}}{2}$R,
ON=$\sqrt{O{C}^{2}-C{N}^{2}}$=$\frac{1}{2}$R,
∴线段MN的最大值为$\frac{\sqrt{2}}{2}$R+$\frac{1}{2}$R,
最小值为$\frac{\sqrt{2}}{2}$R-$\frac{1}{2}$R.
故答案为:$\frac{\sqrt{2}}{2}$R+$\frac{1}{2}$R;$\frac{\sqrt{2}}{2}$R-$\frac{1}{2}$R.
点评 本题考查的是垂径定理和勾股定理的应用,掌握平分弦(不是直径)的直径垂直于弦是解题的关键.

练习册系列答案
相关题目
6.在△ABC中,已知b=7,c=2,B=150°,则a等于( )
| A. | 3$\sqrt{3}$ | B. | 4$\sqrt{3}$ | C. | 5$\sqrt{3}$ | D. | 6$\sqrt{3}$ |
 若a、b、c三数在数轴上对应位置如图所示,化简|a|-|a+b|+|c-b|+|a+c|.
若a、b、c三数在数轴上对应位置如图所示,化简|a|-|a+b|+|c-b|+|a+c|.