题目内容
6.在△ABC中,已知b=7,c=2,B=150°,则a等于( )| A. | 3$\sqrt{3}$ | B. | 4$\sqrt{3}$ | C. | 5$\sqrt{3}$ | D. | 6$\sqrt{3}$ |
分析 作AD⊥CB于D,则∠D=90°,求出∠ABD=30°,由含30°角的直角三角形的性质得出AD=$\frac{1}{2}$AB=1,BD=$\sqrt{3}$AD=$\sqrt{3}$,在Rt△ACD中,由勾股定理得出方程,解方程即可.
解答 解:如图所示: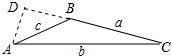
作AD⊥CB于D,
则∠D=90°,
∵∠ABC=150°,
∴∠ABD=30°,
∴AD=$\frac{1}{2}$AB=1,BD=$\sqrt{3}$AD=$\sqrt{3}$,
∴CD=a+$\sqrt{3}$,
在Rt△ACD中,由勾股定理得:AD2+CD2=AC2,
即12+(a+$\sqrt{3}$)2=72,
解得:a=3$\sqrt{3}$,或a=-5$\sqrt{3}$(负值舍去),
∴a=3$\sqrt{3}$;
故选:A.
点评 本题考查了勾股定理、含30°角的直角三角形的性质等知识;本题有一定难度,由勾股定理得出方程是解决问题的关键.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
16.下表是我国长江某段在汛期一周的水位变化情况(单位:m).
注:长江此段的警戒水位为35.50米,“+”表示比警戒水位高,“-”表示比警戒水位低.
问长江该河段本周水位最高的一天是哪天?最低的一天是哪天?为什么?
| 星 期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 水位记录 | +2.40 | +0.60 | -4.00 | -1.60 | +3.50 | +2.00 | -1.50 |
问长江该河段本周水位最高的一天是哪天?最低的一天是哪天?为什么?
 如图,用5种不同的颜色着色,相邻部分不能用同一种颜色,但同一种颜色可以反复使用,则所有不同的着色方法有540种.
如图,用5种不同的颜色着色,相邻部分不能用同一种颜色,但同一种颜色可以反复使用,则所有不同的着色方法有540种. 如图,AB∥CD,∠CDE=140°,则∠A的度数为40.
如图,AB∥CD,∠CDE=140°,则∠A的度数为40.