题目内容
6.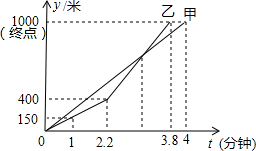 端午节至,甲、乙两队举行了一年一度的赛龙舟比赛,两队在比赛时的路程S(米)与时间t(分钟)之间的函数关系图象如图所示,请你根据图象,回答下列问题:
端午节至,甲、乙两队举行了一年一度的赛龙舟比赛,两队在比赛时的路程S(米)与时间t(分钟)之间的函数关系图象如图所示,请你根据图象,回答下列问题:(1)这次龙舟赛的全程是1000米,乙队先到达终点;
(2)求乙与甲相遇时乙的速度;
(3)求出在乙队与甲相遇之前,他们何时相距100米?
分析 (1)根据函数图象的纵坐标,可得比赛的路程,根据函数图象的横坐标,可得比赛的结果;
(2)根据乙加速后行驶的路程除以加速后的时间,可得答案;
(3)分类讨论,0≤x≤1,1<x≤2.2,乙加速后,根据甲的路程减去乙的路程,可得关于x的方程,根据解方程,可得答案.
解答 解:(1)由纵坐标看出,这次龙舟赛的全程是1000米,
由横坐标看出,乙队先到达终点.
故答案为:1000,乙;
(2)由图象看出,相遇是在乙加速后,加速后的路程是1000-400=600米,加速后的时间时3.8-2.2=1.6分钟,
乙与甲相遇时乙的速度600÷1.6=375米/分钟;
(3)①0≤x≤1时,设行驶x分钟时,甲乙相距100米,
$\frac{1000}{4}$x-$\frac{150}{1}$x=100,
解得x=1;
②1<x≤2.2时,乙加速前,设行驶x分钟时,甲乙相距100米,
$\frac{1000}{4}$x-$\frac{400-150}{2.2-1}$x=100-100,
解得x=0(舍去);
③乙加速后,设行驶x分钟时,甲乙相距100米,
∵$\frac{1000}{4}$×2.2=550,
∴$\frac{1000-400}{3.8-2.2}$x-$\frac{1000}{4}$x=550-400-100.
解得x=0.4,
∴行驶了2.2+0.4=2.6,
答:在乙队与甲相遇之前,他们行驶1分钟或2.6分钟时相距100米.
点评 本题考查了函数图象,分类讨论是解题关键,乙加速前的速度,乙加速后的速度,注意相遇时的速度是加速后的速度.

练习册系列答案
相关题目
2.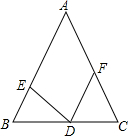 如图所示,在△ABC中,D,E,F分别在BC,AB,AC上,且AB=AC,BE=CD,BD=CF,则∠EDF等于( )
如图所示,在△ABC中,D,E,F分别在BC,AB,AC上,且AB=AC,BE=CD,BD=CF,则∠EDF等于( )
 如图所示,在△ABC中,D,E,F分别在BC,AB,AC上,且AB=AC,BE=CD,BD=CF,则∠EDF等于( )
如图所示,在△ABC中,D,E,F分别在BC,AB,AC上,且AB=AC,BE=CD,BD=CF,则∠EDF等于( )| A. | 180°-2∠B | B. | 180°-∠B | C. | ∠B | D. | 90°-∠B |
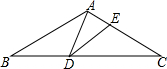 如图,等腰△ABC的腰长为2$\sqrt{3}$,D为底边BC上一点,且BD=2,E为腰AC上一点,若∠ADE=∠B=30°,则CE的长为$\frac{4\sqrt{3}}{3}$.
如图,等腰△ABC的腰长为2$\sqrt{3}$,D为底边BC上一点,且BD=2,E为腰AC上一点,若∠ADE=∠B=30°,则CE的长为$\frac{4\sqrt{3}}{3}$.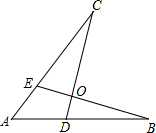 如图.下面四个条件中,请你选出三个,以其中两个为已知条件,另一个为求证,编一道题并证明(只需写出一种情况).①AE=AD;②AB=AC;③OB=OC;④∠B=∠C.
如图.下面四个条件中,请你选出三个,以其中两个为已知条件,另一个为求证,编一道题并证明(只需写出一种情况).①AE=AD;②AB=AC;③OB=OC;④∠B=∠C.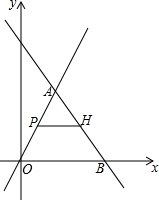 如图,在平面直角坐标系中,直线y=2x上有一点A,点A的横坐标为2,直线y=kx+b经过点A与x轴正半轴交于点B.△AOB的面积为10,点P是线段OA上一动点,过点P作PH∥x轴交线段AB于H,点P的纵坐标为m.
如图,在平面直角坐标系中,直线y=2x上有一点A,点A的横坐标为2,直线y=kx+b经过点A与x轴正半轴交于点B.△AOB的面积为10,点P是线段OA上一动点,过点P作PH∥x轴交线段AB于H,点P的纵坐标为m. 如图,AB是⊙O的直径,点D在AB的延长线上,DC切⊙O于点C,若∠ACD=120°,则∠A=30°.
如图,AB是⊙O的直径,点D在AB的延长线上,DC切⊙O于点C,若∠ACD=120°,则∠A=30°.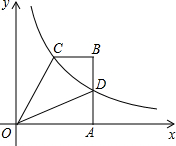 四边形OABC中,BC∥OA,∠OAB=90°,OA=6,腰AB上有一点D,AD=3,四边形ODBC的面积为18,建立如图所示的平面直角坐标系,反比例函数y=$\frac{m}{x}$(x>0)的图象恰好经过点C和点D.
四边形OABC中,BC∥OA,∠OAB=90°,OA=6,腰AB上有一点D,AD=3,四边形ODBC的面积为18,建立如图所示的平面直角坐标系,反比例函数y=$\frac{m}{x}$(x>0)的图象恰好经过点C和点D.