题目内容
11. 如图,AB是⊙O的直径,点D在AB的延长线上,DC切⊙O于点C,若∠ACD=120°,则∠A=30°.
如图,AB是⊙O的直径,点D在AB的延长线上,DC切⊙O于点C,若∠ACD=120°,则∠A=30°.
分析 根据切线的性质得∠OCD=90°,则∠ACO=∠ACD-∠OCD=30°,然后根据等腰三角形的性质即可得到∠A=∠ACO=30°.
解答  解:连结OC,如图,
解:连结OC,如图,
∵DC切⊙O于点C,
∴OC⊥CD,
∴∠OCD=90°,
∵∠ACD=120°,
∴∠ACO=120°-90°=30°,
而OA=OC,
∴∠A=∠ACO=30°.
故答案为30°.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.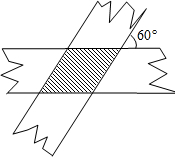 如图,小华剪了两条宽均为$\sqrt{3}$的纸条,交叉叠放在一起,且它们的交角为60°,则它们重叠部分的面积为( )
如图,小华剪了两条宽均为$\sqrt{3}$的纸条,交叉叠放在一起,且它们的交角为60°,则它们重叠部分的面积为( )
 如图,小华剪了两条宽均为$\sqrt{3}$的纸条,交叉叠放在一起,且它们的交角为60°,则它们重叠部分的面积为( )
如图,小华剪了两条宽均为$\sqrt{3}$的纸条,交叉叠放在一起,且它们的交角为60°,则它们重叠部分的面积为( )| A. | $\sqrt{2}$ | B. | 1 | C. | $\frac{2}{3}$$\sqrt{3}$ | D. | 2$\sqrt{3}$ |
20. 如图,是我县2013年11月份某天的天气预报,则这一天的最高气温比最低气温高( )
如图,是我县2013年11月份某天的天气预报,则这一天的最高气温比最低气温高( )
 如图,是我县2013年11月份某天的天气预报,则这一天的最高气温比最低气温高( )
如图,是我县2013年11月份某天的天气预报,则这一天的最高气温比最低气温高( )| A. | -10℃ | B. | 10℃ | C. | 14℃ | D. | -14℃ |
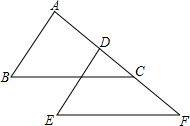 如图,AD=CF,BC=EF,BC∥EF,则AB,DE有什么关系?请说明.
如图,AD=CF,BC=EF,BC∥EF,则AB,DE有什么关系?请说明.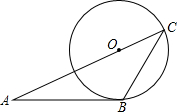 如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC,若∠ABC=120°,OC=6,则$\widehat{BC}$的长为( )
如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC,若∠ABC=120°,OC=6,则$\widehat{BC}$的长为( )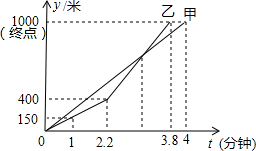 端午节至,甲、乙两队举行了一年一度的赛龙舟比赛,两队在比赛时的路程S(米)与时间t(分钟)之间的函数关系图象如图所示,请你根据图象,回答下列问题:
端午节至,甲、乙两队举行了一年一度的赛龙舟比赛,两队在比赛时的路程S(米)与时间t(分钟)之间的函数关系图象如图所示,请你根据图象,回答下列问题: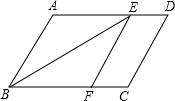 如图,在平行四边形ABCD中,∠ABC的平分线交AD于点E,过E作EF∥AB交BC于点F.
如图,在平行四边形ABCD中,∠ABC的平分线交AD于点E,过E作EF∥AB交BC于点F.