题目内容
2.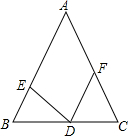 如图所示,在△ABC中,D,E,F分别在BC,AB,AC上,且AB=AC,BE=CD,BD=CF,则∠EDF等于( )
如图所示,在△ABC中,D,E,F分别在BC,AB,AC上,且AB=AC,BE=CD,BD=CF,则∠EDF等于( )| A. | 180°-2∠B | B. | 180°-∠B | C. | ∠B | D. | 90°-∠B |
分析 由条件AB=AC可以得出∠B=∠C,就可以得出△BDE≌△CFD,就可以得出∠BED=∠CDF,∠BDE=∠CFD,由平角的定义就可以得出∠EDF=∠B.
解答 解:∵AB=AC,
∴∠B=∠C.
在△BDE和△CFD中
$\left\{\begin{array}{l}{BE=CD}\\{∠B=∠C}\\{BD=CF}\end{array}\right.$,
∴△BDE≌△CFD(SAS),
∴∠BED=∠CDF,∠BDE=∠CFD.
∴∠BED+∠BDE=∠CDF+∠CFD.
∵∠BED+∠BDE+∠B=∠CDF+∠CFD+∠EDF=180°,
∴∠B=∠EDF.
故选B.
点评 本题考查了等腰三角形的性质的运用,全等三角形的判定及性质的运用,三角形内角和定理的运用,平角的定义的运用,解答时证明三角形全等是关键.

练习册系列答案
相关题目
 如图,已知等腰梯形ABCD中,AD∥BC,AB=DC,点E为BC的中点,求证:AE=DE.
如图,已知等腰梯形ABCD中,AD∥BC,AB=DC,点E为BC的中点,求证:AE=DE.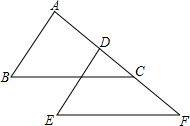 如图,AD=CF,BC=EF,BC∥EF,则AB,DE有什么关系?请说明.
如图,AD=CF,BC=EF,BC∥EF,则AB,DE有什么关系?请说明. 如图,有长为24m的篱笆,围成中间隔有一道篱笆的长方形花圃,且花圃的长可借用一段墙体(墙体的最大可用长度a=10m).
如图,有长为24m的篱笆,围成中间隔有一道篱笆的长方形花圃,且花圃的长可借用一段墙体(墙体的最大可用长度a=10m).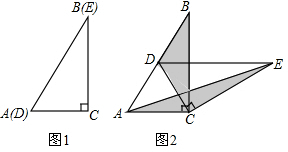
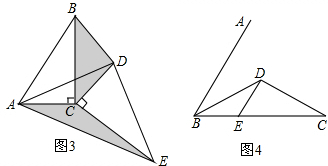 (1)操作发现
(1)操作发现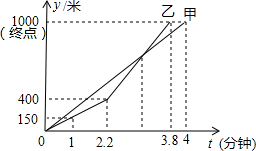 端午节至,甲、乙两队举行了一年一度的赛龙舟比赛,两队在比赛时的路程S(米)与时间t(分钟)之间的函数关系图象如图所示,请你根据图象,回答下列问题:
端午节至,甲、乙两队举行了一年一度的赛龙舟比赛,两队在比赛时的路程S(米)与时间t(分钟)之间的函数关系图象如图所示,请你根据图象,回答下列问题: