题目内容
15.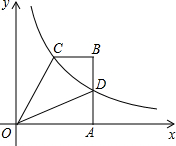 四边形OABC中,BC∥OA,∠OAB=90°,OA=6,腰AB上有一点D,AD=3,四边形ODBC的面积为18,建立如图所示的平面直角坐标系,反比例函数y=$\frac{m}{x}$(x>0)的图象恰好经过点C和点D.
四边形OABC中,BC∥OA,∠OAB=90°,OA=6,腰AB上有一点D,AD=3,四边形ODBC的面积为18,建立如图所示的平面直角坐标系,反比例函数y=$\frac{m}{x}$(x>0)的图象恰好经过点C和点D.(1)求反比例函数关系式;
(2)求出点C的坐标;
(3)在x轴上是否存在点P,使得△CDP是等腰三角形?若存在,直接写出点P的坐标;若不存在,请说明理由.
分析 (1)首先求出点D的坐标,再求出m的值,进而得解;
(2)根据四边形ODBC的面积和△AOD的面积求出四边形OABC的面积,再设出点C的坐标,进而得解;
(3)分PC=PD和CD=PD两种情况考虑,即可得解.
解答 解:(1)∵OA=6,AD=3,∴D点的坐标为(6,3),
∴m=6×3=18,
∴反比例函数的解析式为:y=$\frac{18}{x}$;
(2)S△AOD=$\frac{1}{2}•OA•AD$=$\frac{1}{2}$×6×3=9,
四边形OABC的面积=四边形ODBC的面积+S△AOD=18+9=27,
即:$\frac{(CB+OA)•AB}{2}$=27,
设点C的坐标为(a,$\frac{18}{a}$),
∵BC∥OA,
∴BC=6-a,AB=$\frac{18}{a}$,
∴$\frac{(6-a+6)•\frac{18}{a}}{2}$=27,
解得:a=3,$\frac{18}{a}$=6,∴点C的坐标为(3,6);
(3)P点的坐标为(0,0)或(3,0).
点评 本题主要考查了利用待定系数法求反比例函数的解析式,以及反比例函数与四边形面积的综合性问题,难度比较大,是经常考查的题目,要注意认真总结.

练习册系列答案
相关题目
20. 如图,是我县2013年11月份某天的天气预报,则这一天的最高气温比最低气温高( )
如图,是我县2013年11月份某天的天气预报,则这一天的最高气温比最低气温高( )
 如图,是我县2013年11月份某天的天气预报,则这一天的最高气温比最低气温高( )
如图,是我县2013年11月份某天的天气预报,则这一天的最高气温比最低气温高( )| A. | -10℃ | B. | 10℃ | C. | 14℃ | D. | -14℃ |
5.“羊”字象征吉祥和美好,图的图案与羊有关,其中是轴对称图形的个数是( )


| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
 (1)操作发现
(1)操作发现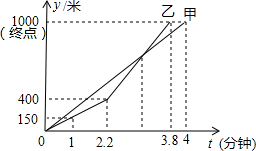 端午节至,甲、乙两队举行了一年一度的赛龙舟比赛,两队在比赛时的路程S(米)与时间t(分钟)之间的函数关系图象如图所示,请你根据图象,回答下列问题:
端午节至,甲、乙两队举行了一年一度的赛龙舟比赛,两队在比赛时的路程S(米)与时间t(分钟)之间的函数关系图象如图所示,请你根据图象,回答下列问题: 如图,在△ABC中,∠C=90°,CA=CB,D是AB的中点,点E、F在AB、AC边上运动(点E不与A、C重合),且保持AE=CF,连接DE,DF,EF.有下列结论:
如图,在△ABC中,∠C=90°,CA=CB,D是AB的中点,点E、F在AB、AC边上运动(点E不与A、C重合),且保持AE=CF,连接DE,DF,EF.有下列结论: