题目内容
5.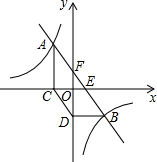 如图,点A(a,$\frac{20}{3}$)和点B(5,-4)都在反比例函数y=$\frac{k}{x}$(k≠0)的图象上,过点A,B的直线与x轴交与点E,与y轴交与点F,过点A作AC⊥x轴于点C,过点B作BD⊥y轴于点D,连接CD.
如图,点A(a,$\frac{20}{3}$)和点B(5,-4)都在反比例函数y=$\frac{k}{x}$(k≠0)的图象上,过点A,B的直线与x轴交与点E,与y轴交与点F,过点A作AC⊥x轴于点C,过点B作BD⊥y轴于点D,连接CD.(1)求点A的坐标及直线AB的解析式;
(2)求四边形ACDB的面积S;
(3)试判断四边形CDBE的形状,并说明理由.
分析 (1)由点A(a,$\frac{20}{3}$)和点B(5,-4)都在反比例函数y=$\frac{k}{x}$(k≠0)的图象上,首先求得解析式,继而求得点A的坐标;然后设直线AB的解析式为:y=mx+n,利用待定系数法即可求得直线AB的解析式;
(2)由(1)可求得各点的坐标,然后易证得四边形CDBE是平行四边形,利用S四边形ACDB=S△ACE+S?CDBE,即可求得答案;
(3)由(2)可得四边形CDBE是平行四边形,易得CD=CE=5,即可判定四边形CDBE是菱形.
解答 解:(1)∵点B(5,-4)在反比例函数y=$\frac{k}{x}$(k≠0)的图象上,
∴k=xy=5×(-4)=-20,
∴反比例函数的解析式为:y=-$\frac{20}{x}$,
∵点A(a,$\frac{20}{3}$)在反比例函数y=$\frac{k}{x}$(k≠0)的图象上,
∴$\frac{20}{3}$a=-20,
解得:a=-3,
∴点A的坐标为:(-3,$\frac{20}{3}$);
设直线AB的解析式为:y=mx+n,
则$\left\{\begin{array}{l}{-3m+n=\frac{20}{3}}\\{5m+n=-4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=-\frac{4}{3}}\\{n=\frac{8}{3}}\end{array}\right.$,
∴直线AB的解析式为:y=-$\frac{4}{3}$x+$\frac{8}{3}$;
(2)∵AC⊥x轴,BD⊥y轴,
∴点C的坐标为:(-3,0),点D的坐标为:(0,-4),
∴OC=3,OD=4,
∵直线AB交x轴于点E,
∴点E的坐标为:(2,0),
∴CE=OC+OE=5,AC=$\frac{20}{3}$,BD=5,OD=4,
∴BD=CE,
∵BD∥CE,
∴四边形CDBE是平行四边形,
∴S四边形ACDB=S△ACE+S?CDBE=$\frac{1}{2}$×5×$\frac{20}{3}$+5×4=$\frac{110}{3}$;
(3)四边形CDBE是菱形.
理由:∵CD=$\sqrt{O{C}^{2}+O{D}^{2}}$=5,
∴CD=CE=5,
∵四边形CDBE是平行四边形,
∴?CDBE是菱形.
点评 此题属于反比例函数综合题,考查了待定系数求函数解析式、四边形的面积问题以及菱形的判定等知识.注意掌握利用割补的方法求面积是关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 36° | B. | 45° | C. | 55° | D. | 60° |
| A. | 38×104 | B. | 3.8×105 | C. | 3.8×104 | D. | 38×105 |
| A. | $\frac{6800}{x}$-6=$\frac{6800}{x+34}$+4 | B. | $\frac{6800}{x}$+6=$\frac{6800}{x+34}$-4 | ||
| C. | $\frac{6800}{x+34}$-6=$\frac{6800}{x}$+4 | D. | $\frac{6800}{x+34}$+6=$\frac{6800}{x}$-4 |
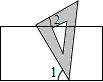 如图,小明把一块含有60°角的直角三角板的两个顶点分别放在矩形的一组对边上,并测得∠1=55°,则∠2的度数是( )
如图,小明把一块含有60°角的直角三角板的两个顶点分别放在矩形的一组对边上,并测得∠1=55°,则∠2的度数是( )| A. | 45° | B. | 27.5° | C. | 30° | D. | 35° |
| A. | 3cm | B. | 11cm | C. | 20cm | D. | 24cm |
 如图,△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF.若∠A=60°,∠ACF=48°,则∠ABC的度数为( )
如图,△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF.若∠A=60°,∠ACF=48°,则∠ABC的度数为( )| A. | 48° | B. | 36° | C. | 30° | D. | 24° |
 如图,在?ABCD中,小平行四边形沿对角线AC平移两次就到了图中的位置(阴影部分),若小平行四边形的面积是2,则?ABCD面积是18.
如图,在?ABCD中,小平行四边形沿对角线AC平移两次就到了图中的位置(阴影部分),若小平行四边形的面积是2,则?ABCD面积是18.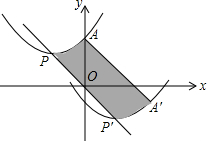 如图,抛物线的顶点为P(-3,3)与y轴交于点A(0,4).若平移该抛物线使其顶点P沿直线移动到点P′(3,-3),点A的对应点为A′,则抛物线上PA段扫过的区域(阴影部分)的面积为24.
如图,抛物线的顶点为P(-3,3)与y轴交于点A(0,4).若平移该抛物线使其顶点P沿直线移动到点P′(3,-3),点A的对应点为A′,则抛物线上PA段扫过的区域(阴影部分)的面积为24.