题目内容
10.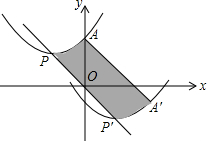 如图,抛物线的顶点为P(-3,3)与y轴交于点A(0,4).若平移该抛物线使其顶点P沿直线移动到点P′(3,-3),点A的对应点为A′,则抛物线上PA段扫过的区域(阴影部分)的面积为24.
如图,抛物线的顶点为P(-3,3)与y轴交于点A(0,4).若平移该抛物线使其顶点P沿直线移动到点P′(3,-3),点A的对应点为A′,则抛物线上PA段扫过的区域(阴影部分)的面积为24.
分析 根据平移的性质得出四边形APP′A′是平行四边形,进而得出AD,PP′的长,求出面积即可.
解答 解:连接AP,A′P′,过点A作AD⊥PP′于点D,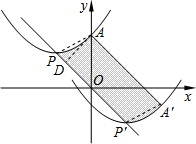
由题意可得出:AP∥A′P′,AP=A′P′,
∴四边形APP′A′是平行四边形,
∵抛物线的顶点为P(-3,3),与y轴交于点A(0,4),平移该抛物线使其顶点P沿直线移动到点P′(3,-3),
∴PO=3$\sqrt{2}$,∠AOP=45°,
又∵AD⊥OP,
∴△ADO是等腰直角三角形,
∴PP′=3$\sqrt{2}$×2=6$\sqrt{2}$,
∴AD=DO=sin45°•OA=$\frac{\sqrt{2}}{2}$×4=2$\sqrt{2}$,
∴抛物线上PA段扫过的区域(阴影部分)的面积为:6$\sqrt{2}$×2$\sqrt{2}$=24.
故答案为24.
点评 此题主要考查了二次函数图象与几何变换以及平行四边形面积求法和勾股定理等知识,根据已知得出AD,PP′是解题关键.

练习册系列答案
相关题目
1.某公司的两名员工甲、乙住在同一个小区,距离公司的距离是5000m,甲每天早上7:00准时从家骑自行车去上班,乙每天早上7:10准时从家骑自行车去上班,两人刚好能在公司门口相遇,已知乙的骑车速度是甲的1.5倍.设甲的骑车速度为xm/min,则可列方程得( )
| A. | $\frac{5000}{x}$-$\frac{5000}{1.5x}$=10 | B. | $\frac{5000}{x}$-$\frac{5000}{1.5x}$=10×60 | ||
| C. | $\frac{5000}{1.5x}$-$\frac{5000}{x}$=10 | D. | $\frac{5000}{1.5x}$-$\frac{5000}{x}$=10×60 |
18.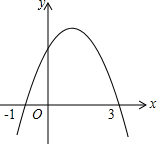 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:①二次函数的图象关于直线x=1对称;②$\frac{b}{c}=\frac{3}{2}$;③-1和3是方程ax2+bx+c=0(a≠0)的两个根;④当x>0时,y随x的增大而增大,其中正确的有( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:①二次函数的图象关于直线x=1对称;②$\frac{b}{c}=\frac{3}{2}$;③-1和3是方程ax2+bx+c=0(a≠0)的两个根;④当x>0时,y随x的增大而增大,其中正确的有( )
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:①二次函数的图象关于直线x=1对称;②$\frac{b}{c}=\frac{3}{2}$;③-1和3是方程ax2+bx+c=0(a≠0)的两个根;④当x>0时,y随x的增大而增大,其中正确的有( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:①二次函数的图象关于直线x=1对称;②$\frac{b}{c}=\frac{3}{2}$;③-1和3是方程ax2+bx+c=0(a≠0)的两个根;④当x>0时,y随x的增大而增大,其中正确的有( )| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
15.下列四个数中,最小的数是( )
| A. | -$\sqrt{2}$ | B. | 0 | C. | 1 | D. | -$\frac{1}{2}$ |
20.下列运算中正确的是( )
| A. | a2+a3=a5 | B. | a2•a4=a8 | C. | a6÷a2=a3 | D. | (a2)3=a6 |
 如图,矩形ABCD的对角线BD在数轴上,表示0的点恰为AC与BD的交点,若点B对应的数为-2,则AC的长为4.
如图,矩形ABCD的对角线BD在数轴上,表示0的点恰为AC与BD的交点,若点B对应的数为-2,则AC的长为4.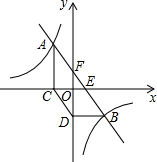 如图,点A(a,$\frac{20}{3}$)和点B(5,-4)都在反比例函数y=$\frac{k}{x}$(k≠0)的图象上,过点A,B的直线与x轴交与点E,与y轴交与点F,过点A作AC⊥x轴于点C,过点B作BD⊥y轴于点D,连接CD.
如图,点A(a,$\frac{20}{3}$)和点B(5,-4)都在反比例函数y=$\frac{k}{x}$(k≠0)的图象上,过点A,B的直线与x轴交与点E,与y轴交与点F,过点A作AC⊥x轴于点C,过点B作BD⊥y轴于点D,连接CD.