题目内容
15.一个正多边形的内角和与其外角和之和是1440°,则这个正多边形的一个外角的度数为( )| A. | 36° | B. | 45° | C. | 55° | D. | 60° |
分析 根据正多边形的内角和为(n-2)×180°,外角和为360°,列方程求解即可解答.
解答 解:设这个正多边形的边数为n,则
(n-2)×180°+360°=1440°,
n-2=6,
∴n=8.
则这个正多边形的一个外角的度数为:360°÷8=45°,
故选;B.
点评 考查了正多边形的内角和的公式和外角和.解决本题的关键是熟记多边形内角和定理:[n-2)•180° (n≥3)且n为整数],外角和为360°.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
3.-3n=(-3)n成立的条件是( )
| A. | n为奇数 | B. | n是正整数 | C. | n是偶数 | D. | n是负数 |
10. 如图,点O在直线AB上,CO⊥DO,垂足为O,则∠1与∠2的度数和为( )
如图,点O在直线AB上,CO⊥DO,垂足为O,则∠1与∠2的度数和为( )
 如图,点O在直线AB上,CO⊥DO,垂足为O,则∠1与∠2的度数和为( )
如图,点O在直线AB上,CO⊥DO,垂足为O,则∠1与∠2的度数和为( )| A. | 45° | B. | 60° | C. | 90° | D. | 无法确定 |
4.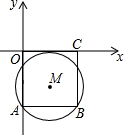 如图,在平面直角坐标系中,正方形ABCO的顶点A、C分别在y轴、x轴上,以AB为弦的⊙M与x轴相切,若点A的坐标为(0,-4),则圆心M的坐标为( )
如图,在平面直角坐标系中,正方形ABCO的顶点A、C分别在y轴、x轴上,以AB为弦的⊙M与x轴相切,若点A的坐标为(0,-4),则圆心M的坐标为( )
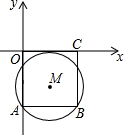 如图,在平面直角坐标系中,正方形ABCO的顶点A、C分别在y轴、x轴上,以AB为弦的⊙M与x轴相切,若点A的坐标为(0,-4),则圆心M的坐标为( )
如图,在平面直角坐标系中,正方形ABCO的顶点A、C分别在y轴、x轴上,以AB为弦的⊙M与x轴相切,若点A的坐标为(0,-4),则圆心M的坐标为( )| A. | (-2,2.5) | B. | (2,-1.5) | C. | (2.5,-2) | D. | (2,-2.5) |
 如图,⊙O的半径为1cm,弦CD的长度1cm,弦AC、BD所夹的锐角α为75°,则弦AB的长为$\sqrt{2}$.
如图,⊙O的半径为1cm,弦CD的长度1cm,弦AC、BD所夹的锐角α为75°,则弦AB的长为$\sqrt{2}$.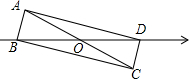 如图,矩形ABCD的对角线BD在数轴上,表示0的点恰为AC与BD的交点,若点B对应的数为-2,则AC的长为4.
如图,矩形ABCD的对角线BD在数轴上,表示0的点恰为AC与BD的交点,若点B对应的数为-2,则AC的长为4. 周末,墨墨用6个相同的小正方体积木搭成了如图所示的几何体,当从左边看这个几何体时,看到的图形应是( )
周末,墨墨用6个相同的小正方体积木搭成了如图所示的几何体,当从左边看这个几何体时,看到的图形应是( )



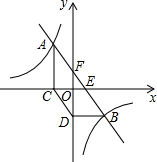 如图,点A(a,$\frac{20}{3}$)和点B(5,-4)都在反比例函数y=$\frac{k}{x}$(k≠0)的图象上,过点A,B的直线与x轴交与点E,与y轴交与点F,过点A作AC⊥x轴于点C,过点B作BD⊥y轴于点D,连接CD.
如图,点A(a,$\frac{20}{3}$)和点B(5,-4)都在反比例函数y=$\frac{k}{x}$(k≠0)的图象上,过点A,B的直线与x轴交与点E,与y轴交与点F,过点A作AC⊥x轴于点C,过点B作BD⊥y轴于点D,连接CD.