题目内容
15. 如图,△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF.若∠A=60°,∠ACF=48°,则∠ABC的度数为( )
如图,△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF.若∠A=60°,∠ACF=48°,则∠ABC的度数为( )| A. | 48° | B. | 36° | C. | 30° | D. | 24° |
分析 根据角平分线的性质可得∠DBC=∠ABD,再根据线段垂直平分线的性质可得BF=CF,进而可得∠FCE=24°,然后可算出∠ABC的度数.
解答 解:∵BD平分∠ABC,
∴∠DBC=∠ABD,
∵∠A=60°,
∴∠ABC+∠ACB=120°,
∵∠ACF=48°,
∵BC的中垂线交BC于点E,
∴BF=CF,
∴∠FCB=∠FBC,
∴∠ABC=2∠FCE,
∵∠ACF=48°,
∴3∠FCE=120°-48°=72°,
∴∠FCE=24°,
∴∠ABC=48°,
故选:A.
点评 此题主要考查了线段垂直平分线的性质,以及三角形内角和定理,关键是掌握线段垂直平分线上任意一点,到线段两端点的距离相等.

练习册系列答案
相关题目
6.多项式x2-1与多项式x2-2x+1的公因式是( )
| A. | x-1 | B. | x+1 | C. | x2-1 | D. | (x-1)2 |
20.下列运算中正确的是( )
| A. | a2+a3=a5 | B. | a2•a4=a8 | C. | a6÷a2=a3 | D. | (a2)3=a6 |
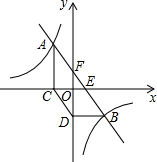 如图,点A(a,$\frac{20}{3}$)和点B(5,-4)都在反比例函数y=$\frac{k}{x}$(k≠0)的图象上,过点A,B的直线与x轴交与点E,与y轴交与点F,过点A作AC⊥x轴于点C,过点B作BD⊥y轴于点D,连接CD.
如图,点A(a,$\frac{20}{3}$)和点B(5,-4)都在反比例函数y=$\frac{k}{x}$(k≠0)的图象上,过点A,B的直线与x轴交与点E,与y轴交与点F,过点A作AC⊥x轴于点C,过点B作BD⊥y轴于点D,连接CD. 如图,在平面直角坐标系xOy中,直线y=$\frac{3}{2}$x与双曲线y=$\frac{6}{x}$相交于A,B两点,C是第一象限内双曲线上一点,连接CA并延长交y轴于点P,连接BP,BC.若△PBC的面积是24,则点C的坐标为(6,1).
如图,在平面直角坐标系xOy中,直线y=$\frac{3}{2}$x与双曲线y=$\frac{6}{x}$相交于A,B两点,C是第一象限内双曲线上一点,连接CA并延长交y轴于点P,连接BP,BC.若△PBC的面积是24,则点C的坐标为(6,1).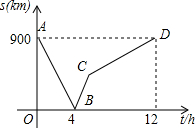 一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地,两车同时出发,快车到达乙地后,快车停止运动,慢车继续以原速匀速驶往甲地,直至慢车到达甲地为止,设慢车行驶的时间为t(h),两车之间的距离为s(km),图中的折线表示s与t之间的函数关系.根据图象提供的信息有下列说法:①甲、乙两地之间的距离为900km;②行驶4h两车相遇;③快车的速度为150km/h;④行驶6h两车相距400km;⑤相遇时慢车行驶了240km;⑥快车共行驶了6h.其中符合图象描述的说法有( )个.
一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地,两车同时出发,快车到达乙地后,快车停止运动,慢车继续以原速匀速驶往甲地,直至慢车到达甲地为止,设慢车行驶的时间为t(h),两车之间的距离为s(km),图中的折线表示s与t之间的函数关系.根据图象提供的信息有下列说法:①甲、乙两地之间的距离为900km;②行驶4h两车相遇;③快车的速度为150km/h;④行驶6h两车相距400km;⑤相遇时慢车行驶了240km;⑥快车共行驶了6h.其中符合图象描述的说法有( )个.