题目内容
一个矩形，两边长分别为xcm和10cm，如果它的周长小于80cm，面积大于100cm2，则x的取值范围是__．
10＜x＜30
【解析】【解析】
矩形的周长是2（x+10）cm，面积是10xcm2．根据题意，得：
，
解不等式：2（x+10）＜80，
解得：x＜30，
解不等式：10x＞100，
解得：x＞10，
所以x的取值范围是：10＜x＜30．
故答案为：10＜x＜30．
应用题作业本系列答案现有同一品牌工艺品100件,其中有2件次品,从中任取一件,( )是次品.
A. 一定 B. 不大可能
C. 很可能 D. 不可能
B
【解析】由于次品在总数中所占的数目较少,所以抽取一次,抽到次品的可能性较小.
故选B. 计算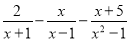
【解析】试题分析：先找出最简公分母，然后把各分式通分，然后按照分母不变，分子相加减的方法进行计算，最后把分子合并同类项，最后结果化成最简．
试题解析：
【解析】
原式＝
＝
＝． 分式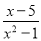
与
的公分母是（ ）
A. 
B. 
C. 
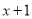D.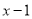 
A
【解析】试题分析：x2－1＝(x＋1)(x－1)，
所以分式与的公分母是(x＋1)(x－1)，
即x2－1．
故选A． 某饮料厂以300千克的A种果汁和240千克的B种果汁为原料，配制生产甲、乙两种新型饮料，已知每千克甲种饮料含0.6千克A种果汁，含0.3千克B种果汁；每千克乙种饮料含0.2千克A种果汁，含0.4千克B种果汁．饮料厂计划生产甲、乙两种新型饮料共650千克，设该厂生产甲种饮料x（千克）．
（1）列出满足题意的关于x的不等式组，并求出x的取值范围；
（2）已知该饮料厂的甲种饮料销售价是每1千克3元，乙种饮料销售价是每1千克4元，那么该饮料厂生产甲、乙两种饮料各多少千克，才能使得这批饮料销售总金额最大？
【解析】
（1）设该厂生产甲种饮料x千克，则生产乙种饮料（650﹣x）千克，
根据题意得，，
由①得，x≤425，由②得，x≥200，
∴x的取值范围是200≤x≤425。
（2）设这批饮料销售总金额为y元，根据题意得，
，即y=﹣x+2600，
∵k=﹣1＜0，
∴当x=200时，这批饮料销售总金额最大，为﹣200+2600=2400元。
【解析... 当正整数m为何值时，关于x的方程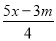
＝
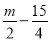的解是非正数？
m＝1或2或3.
【解析】【试题分析】求出不等式＝的解集为 ，再根据方程的解为非正数，得不等式m－3≤0，解不等式得：m≤3，因为m为正整数，m＝1或2或3.
【试题解析】
＝
去分母得：
移项得：
系数化为1 得：
又 m－3≤0，
∴m≤3，
∵m为正整数，
∴m＝1或2或3.
故答案为：m＝1或2或3. 在不等式
＞
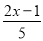的变形过程中：①去分母，得5(2＋x)＞3(2x－1)；②去括号，得10＋5x＞6x－3；③移项得5x－6x＞－3－10；④系数化为1，得x＞13.其中错误的步骤是( )
A. ① B. ②
C. ③ D. ④
D
【解析】＞的变形过程中：①去分母，得5(2＋x)＞3(2x－1)；②去括号，得10＋5x＞6x－3；③移项得5x－6x＞－3－10；④系数化为1，得x<13.故错误的步骤是④.故选D. 为进一步建设秀美、宜居的生态环境，某村欲购买甲、乙、丙三种树美化村庄，已知甲、乙丙三种树的价格之比为2：2：3，甲种树每棵200元，现计划用210000元资金，购买这三种树共1000棵．
（1）求乙、丙两种树每棵各多少元？
（2）若购买甲种树的棵树是乙种树的2倍，恰好用完计划资金，求这三种树各能购买多少棵？
（3）若又增加了10120元的购树款，在购买总棵树不变的前提下，求丙种树最多可以购买多少棵？
（1）200元，200元，（2）能购买甲种树600棵，乙种树300棵，丙种树100棵；（3）丙种树最多可以购买201棵．
【解析】
试题分析：（1）利用已知甲、乙丙三种树的价格之比为2：2：3，甲种树每棵200元，即可求出乙、丙两种树每棵钱数；
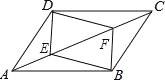
（2）假设购买乙种树x棵，则购买甲种树2x棵，丙种树（1000-3x）棵，利用（1）中所求树木价格以及现计划用210000元资金购买这三... 如图，在?ABCD中，点E，F在对角线AC上，且AE=CF．求证：
（1）DE=BF；
（2）四边形DEBF是平行四边形．
详见解析.
【解析】
试题分析：（1）根据全等三角形的判定方法，判断出△ADE≌△CBF，即可推得DE=BF．（2）首先判断出DE∥BF；然后根据一组对边平行且相等的四边形是平行四边形，推得四边形DEBF是平行四边形即可．
试题解析：（1）∵四边形ABCD是平行四边形，
∴AD∥CB，AD=CB，
∴∠DAE=∠BCF，
在△ADE和△CBF中，
∴△AD...