题目内容
一个多边形的内角和是外角和的2倍，则这个多边形的边数为______．
6
【解析】∵多边形的外角和是360度，多边形的内角和是外角和的2倍，
则内角和是720度，
720÷180+2=6，
∴这个多边形是六边形，
故答案为：6．
练习册系列答案
桃李文化快乐暑假武汉出版社系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
在不等式
＞
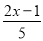的变形过程中：①去分母，得5(2＋x)＞3(2x－1)；②去括号，得10＋5x＞6x－3；③移项得5x－6x＞－3－10；④系数化为1，得x＞13.其中错误的步骤是( )
A. ① B. ②
C. ③ D. ④
D
【解析】＞的变形过程中：①去分母，得5(2＋x)＞3(2x－1)；②去括号，得10＋5x＞6x－3；③移项得5x－6x＞－3－10；④系数化为1，得x<13.故错误的步骤是④.故选D. 小于88的两位正整数，它的个位数字比十位数字大4，这样的两位数有_________个．
5
【解析】设十位数字为x，则个位数字为x+4
依题意得10x+x+4＜88
得x＜
又∵x应为正整数，且大于0；并且0≤个位数字≤9，因而5≤x+4≤9
∴1≤x≤5，故这样的两位数有5个．
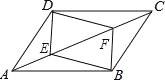
故答案：5. 如图，在?ABCD中，点E，F在对角线AC上，且AE=CF．求证：
（1）DE=BF；
（2）四边形DEBF是平行四边形．
详见解析.
【解析】
试题分析：（1）根据全等三角形的判定方法，判断出△ADE≌△CBF，即可推得DE=BF．（2）首先判断出DE∥BF；然后根据一组对边平行且相等的四边形是平行四边形，推得四边形DEBF是平行四边形即可．
试题解析：（1）∵四边形ABCD是平行四边形，
∴AD∥CB，AD=CB，
∴∠DAE=∠BCF，
在△ADE和△CBF中，
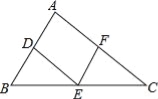
∴△AD... 如图，在△ABC中，点D、E、F分别是边AB、BC、CA上的中点，且AB=6cm，AC=8cm，则四边形ADEF的周长等于 cm．
14.
【解析】
试题分析：∵D、E分别AB、BC的中点，∴AD=AB，DE=AC.同理AF=AC，EF=AB.∴l四边形ADEF=AD+DE+EF+AF=（AB+AC+AB+AC）=AB+AC=14cm. 如图，?ABCD的对角线AC，BD相交于点O，已知AD＝8，BD＝12，AC＝6，则△OBC的周长为( )
A. 13 B. 17 C. 20 D. 26
B
【解析】试题分析：由平行四边形的性质得出OA=OC=3，OB=OD=6，BC=AD=8，即可求出△OBC的周长．
【解析】
∵四边形ABCD是平行四边形，
∴OA=OC=3，OB=OD=6，BC=AD=8，
∴△OBC的周长=OB+OC+AD=3+6+8=17．
故选：B． 在下列条件中，能够判定一个四边形是平行四边形的是（ ）
A. 一组对边平行，另一组对边相等
B. 一组对边相等，一组对角相等
C. 一组对边平行，一条对角线平分另一条对角线
D. 一组对边相等，一条对角线平分另一条对角线
C
【解析】A、错误．这个四边形有可能是等腰梯形．
B、错误．不满足三角形全等的条件，无法证明相等的一组对边平行．
C、正确．可以利用三角形全等证明平行的一组对边相等．故是平行四边形．
D、错误．不满足三角形全等的条件，无法证明相等的一组对边平行．
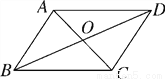
故选C． 如图，?ABCD的对角线AC，BD相交于点O，且AC＋BD＝16，CD＝6，则△ABO的周长是( )
A. 10 B. 14 C. 20 D. 22
B
【解析】试题分析：∵四边形ABCD是平行四边形，∴AO=CO，BO=DO，DC=AB=6，∵AC+BD=16，∴AO+BO=8，∴△ABO的周长是：14．故选B． 平面直角坐标系xOy中，对称轴平行于y轴的抛物线过点A（1，0）、B（3，0）和C（4，6）；
（1）求抛物线的表达式；
（2）现将此抛物线先沿x轴方向向右平移6个单位，再沿y轴方向平移k个单位，若所得抛物线与x轴交于点D、E（点D在点E的左边），且使△ACD∽△AEC（顶点A、C、D依次对应顶点A、E、C），试求k的值，并注明方向．
（1）y=2x2﹣8x+6；（2）向下平移6个单位．
【解析】试题分析：（1）利用待定系数法直接求出抛物线的解析式；
（2）设出D，E坐标，根据平移，用k表示出平移后的抛物线解析式，利用坐标轴上点的特点得出m+n=16，mn=63﹣，进而利用相似三角形得出比例式建立方程即可求出k．
试题解析：【解析】
（1）∵抛物线过点A（1，0）、B（3，0），∴设抛物线的解析式为y=a（x...