题目内容
2.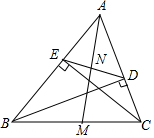 如图,BD、CE是△ABC的两条高,AM是∠BAC的平分线,交BC于M,交DE于N,求证:
如图,BD、CE是△ABC的两条高,AM是∠BAC的平分线,交BC于M,交DE于N,求证:(1)△ABD∽△ACE;
(2)$\frac{AM}{AN}$=$\frac{BC}{DE}$.
分析 (1)先根据有两组角对应相等的两个三角形相似,判定△ABD∽△ACE;
(2)先相似三角形的性质,得出$\frac{AD}{AB}$=$\frac{AE}{AC}$,再根据∠DAE=∠BAC,判定△ADE∽△ABC,进而得到$\frac{BC}{DE}$=$\frac{AC}{AE}$,再根据∠CAM=∠EAN,判定△ACM∽△AEN,得到$\frac{AC}{AE}$=$\frac{AM}{AN}$,最后等量代换即可得到$\frac{AM}{AN}$=$\frac{BC}{DE}$.
解答 证明:(1)∵BD、CE是△ABC的两条高,
∴∠ADB=∠AEC=90°,
∵∠DAE=∠BAC,
∴△ABD∽△ACE;
(2)∵△ABD∽△ACE,
∴$\frac{AD}{AE}$=$\frac{AB}{AC}$,即$\frac{AD}{AB}$=$\frac{AE}{AC}$,
又∵∠DAE=∠BAC,
∴△ADE∽△ABC,
∴$\frac{BC}{DE}$=$\frac{AC}{AE}$,且∠ACB=∠AED,
∵AM是∠BAC的平分线,
∴∠CAM=∠EAN,
∴△ACM∽△AEN,
∴$\frac{AC}{AE}$=$\frac{AM}{AN}$,
∴$\frac{AM}{AN}$=$\frac{BC}{DE}$.
点评 本题主要考查了相似三角形的判定与性质的综合应用,解题时注意:有两组角对应相等的两个三角形相似,两组对应边的比相等且夹角对应相等的两个三角形相似.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
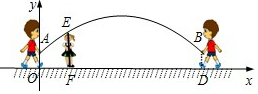 跳绳时,绳甩到最高处时的形状是抛物线.正在甩绳的甲、乙两名同学拿绳的手间距AB为6米,到地面的距离AO和BD均为0.9米,身高为1.4米的小丽站在距点O的水平距离为1米的点F处,绳子甩到最高处时刚好通过她的头顶点E.以点O为原点建立如图所示的平面直角坐标系,设此抛物线的解析式为y=ax2+bx+0.9.
跳绳时,绳甩到最高处时的形状是抛物线.正在甩绳的甲、乙两名同学拿绳的手间距AB为6米,到地面的距离AO和BD均为0.9米,身高为1.4米的小丽站在距点O的水平距离为1米的点F处,绳子甩到最高处时刚好通过她的头顶点E.以点O为原点建立如图所示的平面直角坐标系,设此抛物线的解析式为y=ax2+bx+0.9.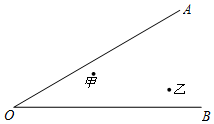 近年来,国家实施农村医疗卫生改革,某县计划在甲村、乙村之问设立一座定点医疗站点P,甲、乙两村坐落在两相交公路内(如图所示).医疗站必须适合下列条件:
近年来,国家实施农村医疗卫生改革,某县计划在甲村、乙村之问设立一座定点医疗站点P,甲、乙两村坐落在两相交公路内(如图所示).医疗站必须适合下列条件: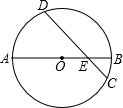 如图,⊙O的直径AB与弦CD交于点E,AE=5,BE=1,CD=4$\sqrt{2}$,求
如图,⊙O的直径AB与弦CD交于点E,AE=5,BE=1,CD=4$\sqrt{2}$,求