��Ŀ����
13��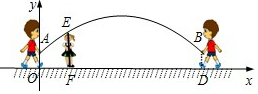 ����ʱ����˦����ߴ�ʱ����״�������ߣ�����˦���ļס�������ͬѧ�������ּ��ABΪ6�ף�������ľ���AO��BD��Ϊ0.9�ף�����Ϊ1.4��С��վ�ھ��O��ˮƽ����Ϊ1�ĵ�F��������˦����ߴ�ʱ�պ�ͨ������ͷ����E���Ե�OΪԭ�㽨����ͼ��ʾ��ƽ��ֱ������ϵ����������ߵĽ���ʽΪy=ax2+bx+0.9��
����ʱ����˦����ߴ�ʱ����״�������ߣ�����˦���ļס�������ͬѧ�������ּ��ABΪ6�ף�������ľ���AO��BD��Ϊ0.9�ף�����Ϊ1.4��С��վ�ھ��O��ˮƽ����Ϊ1�ĵ�F��������˦����ߴ�ʱ�պ�ͨ������ͷ����E���Ե�OΪԭ�㽨����ͼ��ʾ��ƽ��ֱ������ϵ����������ߵĽ���ʽΪy=ax2+bx+0.9����1�����С��վ��OD֮�䣬�����O�ľ���Ϊ3�ף�������˦����ߴ�ʱ�պ�ͨ������ͷ�����������С�������ߣ�
��2���������Ϊ1.4��С��վ��OD֮�䣬�����O�ľ���Ϊt�ף�����˦����ߴ�ʱ��������ͷ��������ͼ��ֱ��д��t��ȡֵ��Χ1��t��5��
���� ��1���������������������ߵĽ���ʽ���Ӷ��������С�������ߣ�
��2�����ݶ��κ������жԳ��Կ��Խ���⣮
��� �⣺��1��������ɵã������߾����㣨1��1.4��������ĺ�����Ϊx=3��
��$\left\{\begin{array}{l}{a��{1}^{2}+b��1+0.9=1.4}\\{-\frac{b}{2a}=3}\end{array}\right.$��
��ã�a=-0.1��b=0.6��
�������ߵĽ���ʽΪy=-0.1x2+0.6x+0.9��
��x=3ʱ��y=-0.1��32+0.6��3+0.9=1.8��
��С����������1.8�ף�
��2���������ߵĶԳ���Ϊֱ��x=3������Ϊ1.4��С��վ�ھ��O��ˮƽ����Ϊ1�ĵ�F��������˦����ߴ�ʱ�պ�ͨ������ͷ����E��
������Ϊ1.4��С��վ��OD֮�䣬�����O�ľ���Ϊt�ף�����˦����ߴ�ʱ��������ͷ��ʱt��ȡֵ��Χ�ǣ�
1��t��5��
�ʴ�Ϊ��1��t��5��
���� ���⿼����κ�����Ӧ�ã�����Ĺؼ�����ȷ���⣬�ҳ�����������Ҫ��������

��ϰ��ϵ�д�
�����Ŀ
3��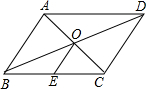 ��ͼ��?ABCD�У��Խ���AC��BD���ڵ�O����E��BC���е㣮��OE=3cm����AB�ij�Ϊ��������
��ͼ��?ABCD�У��Խ���AC��BD���ڵ�O����E��BC���е㣮��OE=3cm����AB�ij�Ϊ��������
 ��ͼ��?ABCD�У��Խ���AC��BD���ڵ�O����E��BC���е㣮��OE=3cm����AB�ij�Ϊ��������
��ͼ��?ABCD�У��Խ���AC��BD���ڵ�O����E��BC���е㣮��OE=3cm����AB�ij�Ϊ��������| A�� | 3 cm | B�� | 6 cm | C�� | 9 cm | D�� | 12 cm |
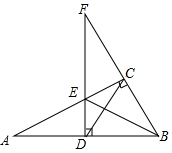 ��Rt��ABC�У���ACB=90�㣬AB�Ĵ�ֱƽ����DE��BC���ӳ����ڵ�F������CD��BE����EF=AE��
��Rt��ABC�У���ACB=90�㣬AB�Ĵ�ֱƽ����DE��BC���ӳ����ڵ�F������CD��BE����EF=AE��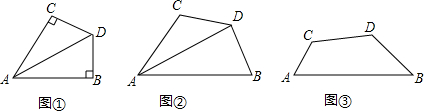
 ��ͼ��ʾ���ѡ�ABC�Ƶ�C˳ʱ����ת35��õ���A��B��C�䣬A��B�佻AC�ڵ�D����֪��A��DC=90�㣬���A�Ķ�����
��ͼ��ʾ���ѡ�ABC�Ƶ�C˳ʱ����ת35��õ���A��B��C�䣬A��B�佻AC�ڵ�D����֪��A��DC=90�㣬���A�Ķ�����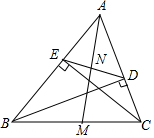 ��ͼ��BD��CE�ǡ�ABC�������ߣ�AM�ǡ�BAC��ƽ���ߣ���BC��M����DE��N����֤��
��ͼ��BD��CE�ǡ�ABC�������ߣ�AM�ǡ�BAC��ƽ���ߣ���BC��M����DE��N����֤��