题目内容
14.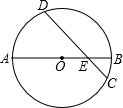 如图,⊙O的直径AB与弦CD交于点E,AE=5,BE=1,CD=4$\sqrt{2}$,求
如图,⊙O的直径AB与弦CD交于点E,AE=5,BE=1,CD=4$\sqrt{2}$,求(1)求圆心O到弦CD的距离;
(2)求CE的长.
分析 过点O作OF⊥CD于点F,连接OD,根据垂径定理和勾股定理即可求出OF、CE的长度.
解答 解:(1) 过点O作OF⊥CD于点F,连接OD
过点O作OF⊥CD于点F,连接OD
∴由垂径定理可知:CF=DF=$\frac{1}{2}$CD=2$\sqrt{2}$,
∵AB=AE+BE=6,
∴OD=$\frac{1}{2}$AB=3,
∴由勾股定理可求得:OF=1,
(2)∵OE=AE-OA=2,
∴由勾股定理可求得:EF=$\sqrt{3}$,
∴CE=CF-EF=2$\sqrt{2}$-$\sqrt{3}$,
点评 本题考查垂径定理,涉及勾股定理,注意若有弦长,通常过圆心作弦的垂线段,然后利用垂径定理进行解答.

练习册系列答案
相关题目
19.数6、-1、15、-3中,最小的数是( )
| A. | 6 | B. | -1 | C. | 15 | D. | -3 |
6.先填写表,通过观察后再回答问题:
(1)表格中x=0.1,y=10;
(2)从表格中探究a与数位的规律,并利用这个规律解决下面两个问题:
①已知$\sqrt{10}$≈3.16,则$\sqrt{1000}$≈31.6;
②已知$\sqrt{m}$=8.973,若$\sqrt{b}$=897.3,用含m的代数式表示b,则b=10000m;
(3)试比较$\sqrt{a}$与a的大小.
| a | … | 0.0001 | 0.01 | 1 | 100 | 10000 | … |
| $\sqrt{a}$ | … | 0.01 | x | 1 | y | 100 | … |
(2)从表格中探究a与数位的规律,并利用这个规律解决下面两个问题:
①已知$\sqrt{10}$≈3.16,则$\sqrt{1000}$≈31.6;
②已知$\sqrt{m}$=8.973,若$\sqrt{b}$=897.3,用含m的代数式表示b,则b=10000m;
(3)试比较$\sqrt{a}$与a的大小.
3.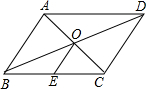 如图,?ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )
如图,?ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )
 如图,?ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )
如图,?ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )| A. | 3 cm | B. | 6 cm | C. | 9 cm | D. | 12 cm |
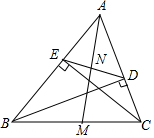 如图,BD、CE是△ABC的两条高,AM是∠BAC的平分线,交BC于M,交DE于N,求证:
如图,BD、CE是△ABC的两条高,AM是∠BAC的平分线,交BC于M,交DE于N,求证: 如图,沿长方形ABCD的对角线AC对折,点B落在点E上,AE与CD交于F点,
如图,沿长方形ABCD的对角线AC对折,点B落在点E上,AE与CD交于F点,