题目内容
 如图,△ABC中,∠B=∠C=70°,BP=CE,BD=CP,求∠DPE的度数.
如图,△ABC中,∠B=∠C=70°,BP=CE,BD=CP,求∠DPE的度数.考点:全等三角形的判定与性质
专题:
分析:此题先判定△DBP与△PCE全等,得出∠BDP与∠EPC相等,再根据三角形的内角和定理求∠DPE的度数.
解答: 解:在△DBP和△PCE中,
解:在△DBP和△PCE中,
,
∴△DBP≌△PCE(SAS),
∴∠BDP=∠EPC,
又∵∠B=70°,
∴∠DPB+∠BDP=110°,
∴∠DPE=180°-(∠DPB+∠EPC)=180°-(∠DPB+∠BDP)=70°.
即∠DPE=70°.
 解:在△DBP和△PCE中,
解:在△DBP和△PCE中,
|
∴△DBP≌△PCE(SAS),
∴∠BDP=∠EPC,
又∵∠B=70°,
∴∠DPB+∠BDP=110°,
∴∠DPE=180°-(∠DPB+∠EPC)=180°-(∠DPB+∠BDP)=70°.
即∠DPE=70°.
点评:本题考查了全等三角形的判定以及全等三角形的性质、等腰三角形的性质以及三角形内角和定理;利用题目中隐含的条件平角解题是解决本题得到关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
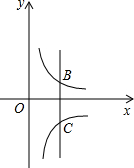 如图,直线x=t(t>0)与反比例函数y=
如图,直线x=t(t>0)与反比例函数y=| 2 |
| x |
| 3 |
| x |
| A、5 | ||
B、
| ||
C、
| ||
| D、不能确定 |
 如图,在△ABC中,DE是中位线,若∠ADE=60°,BC=8cm,则∠B=
如图,在△ABC中,DE是中位线,若∠ADE=60°,BC=8cm,则∠B= 如图,已知∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A4B4A5的边长为( )
如图,已知∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A4B4A5的边长为( ) 如图,在正方形网格中,△ABC各顶点都在格点上,点A,C的坐标分别为(-5,1)、(-1,4),结合所给的平面直角坐标系解答下列问题:
如图,在正方形网格中,△ABC各顶点都在格点上,点A,C的坐标分别为(-5,1)、(-1,4),结合所给的平面直角坐标系解答下列问题: 将如图所示的长方体用过ABCD的平面切割,得到两个什么几何体?说出它们的名称.
将如图所示的长方体用过ABCD的平面切割,得到两个什么几何体?说出它们的名称.