题目内容
已知张村李村分别位于直径为300m的半圆弧上三等分点的位置,现要在河边(直径所在的直线)修水泵站,分别向两村供水,最少需要多少米的水管?画出图形说明理由.
考点:轴对称-最短路线问题,勾股定理,垂径定理的应用
专题:
分析:设M、N是张村李村分别位于的位置,作M关于直径AB的对称点M′,再连接M′N,M′N与AB交于点K,K点就是水泵站的位置,利用了轴对称的性质可得∴∠AOM′=∠AOM=60°,再根据∠AOM′+∠AOM+∠MON=180°,从而确定修水泵站在圆心O的位置,即可得出M′N=OM+ON=AB=300m.
解答:解:设M、N是张村李村分别位于的位置,作M关于直径AB的对称点M′,再连接M′N,M′N与AB交于点K,K点就是水泵站的位置;
∵M、N是半圆弧上三等分点,
∴∠AOM=∠MON=∠BON=60°,
∵M′是M的对称点,
∴∠AOM′=∠AOM=60°,
∴∠AOM′+∠AOM+∠MON=180°,
∴MN必经过O点,
∴K点与O重合,
∴M′N=OM+ON=AB=300m.

∵M、N是半圆弧上三等分点,
∴∠AOM=∠MON=∠BON=60°,
∵M′是M的对称点,
∴∠AOM′=∠AOM=60°,
∴∠AOM′+∠AOM+∠MON=180°,
∴MN必经过O点,
∴K点与O重合,
∴M′N=OM+ON=AB=300m.
点评:此题主要考查了最短路线问题,正确作出图形,确定线路是解决此题的关键,也是难点.在直线L上的同侧有两个点A、B,在直线L上有到A、B的距离之和最短的点存在,可以通过轴对称来确定,即作出其中一点关于直线L的对称点,对称点与另一点的连线与直线L的交点就是所要找的点

练习册系列答案
相关题目
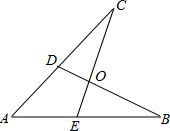 如图,已知AB=AC,要使△ABD≌△ACE,只需补充条件( )
如图,已知AB=AC,要使△ABD≌△ACE,只需补充条件( )| A、∠BOE=∠COD |
| B、∠DOE=∠BOC |
| C、BO=CO |
| D、BO⊥CO |
 如图,△ABC中,∠B=∠C=70°,BP=CE,BD=CP,求∠DPE的度数.
如图,△ABC中,∠B=∠C=70°,BP=CE,BD=CP,求∠DPE的度数. 如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,点B为劣弧AN的中点.点P是直径MN上一动点,求PA+PB的最小值.
如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,点B为劣弧AN的中点.点P是直径MN上一动点,求PA+PB的最小值.