题目内容
 如图,已知∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A4B4A5的边长为( )
如图,已知∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A4B4A5的边长为( )| A、8 | B、16 | C、32 | D、64 |
考点:等边三角形的性质
专题:规律型
分析:由等边三角形的性质可证得A2B1⊥OB1,再根据30°角所对的直角边是斜边的一半可求得A2B1=
OA2,依此类推可求得答案.
| 1 |
| 2 |
解答:解:
∵△A1B1A2为等边三角形,
∴∠B1A1A2=60°,
∵∠MON=30°,
∴∠OB1A2=30°+60°=90°,
∴A2B1=
OA2,
同理可求得:B4A5=
OA5,
∵OA1=1,
∴OA4=2OA3=4OA2=8OA1=8,OA5=2OA4=4OA3=8OA2=16OA1=16,
∴A4A5=OA5-OA4=16-8=8,
故选:A.
∵△A1B1A2为等边三角形,
∴∠B1A1A2=60°,
∵∠MON=30°,
∴∠OB1A2=30°+60°=90°,
∴A2B1=
| 1 |
| 2 |
同理可求得:B4A5=
| 1 |
| 2 |
∵OA1=1,
∴OA4=2OA3=4OA2=8OA1=8,OA5=2OA4=4OA3=8OA2=16OA1=16,
∴A4A5=OA5-OA4=16-8=8,
故选:A.
点评:本题主要考查等边三角形的性质及含30°角的直角三角形的性质,由条件得到OA5=2OA4=4OA3=8OA2=16OA1是解题的关键.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
 如图,△ABC中,∠B=∠C=70°,BP=CE,BD=CP,求∠DPE的度数.
如图,△ABC中,∠B=∠C=70°,BP=CE,BD=CP,求∠DPE的度数.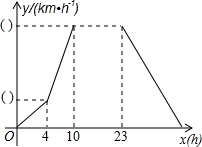 某气象研究中心观测一场沙尘暴从发生到结束的全过程.开始时风速平均每小时增加2km,4h后,沙尘暴经过开阔荒漠地,风速变为平均增加4km/h.一段时间,风速保持不变.当沙尘暴遇到绿色植被区时,其风速平均减小lkm/h,最终停止.结合风速y与时间x的图象(如图),回答下列问题.
某气象研究中心观测一场沙尘暴从发生到结束的全过程.开始时风速平均每小时增加2km,4h后,沙尘暴经过开阔荒漠地,风速变为平均增加4km/h.一段时间,风速保持不变.当沙尘暴遇到绿色植被区时,其风速平均减小lkm/h,最终停止.结合风速y与时间x的图象(如图),回答下列问题. 如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,点B为劣弧AN的中点.点P是直径MN上一动点,求PA+PB的最小值.
如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,点B为劣弧AN的中点.点P是直径MN上一动点,求PA+PB的最小值. 如图,已知∠B=∠C,AD=AE,求证:AB=AC.
如图,已知∠B=∠C,AD=AE,求证:AB=AC.