题目内容
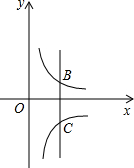 如图,直线x=t(t>0)与反比例函数y=
如图,直线x=t(t>0)与反比例函数y=| 2 |
| x |
| 3 |
| x |
| A、5 | ||
B、
| ||
C、
| ||
| D、不能确定 |
考点:反比例函数系数k的几何意义
专题:
分析:如图,连接OC、OB.设x=t与x轴交于点D.因为△OBC与△ABC是等底同高的两个三角形,所以它们的面积相等.所以由反比例函数系数k的几何意义知
△BOC的面积=
×2+
×|-3|=
.
△BOC的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
解答: 解:如图,如图,连接OC、OB.
解:如图,如图,连接OC、OB.
∵点B、C分别在反比例函数y=
(x>0),y=-
(x>0)的图象上,
∴S△BOC=S△BOD+S△COD=
×2+
×|-3|=
.
∵直线x=t(t>0)与反比例函数y=
(x>0),y=-
(x>0)的图象分别交于B、C两点,A为y轴上的任意一点,(即AB∥y轴),
∴S△BOC=S△ABC=
,
故选:C.
 解:如图,如图,连接OC、OB.
解:如图,如图,连接OC、OB.∵点B、C分别在反比例函数y=
| 2 |
| x |
| 3 |
| x |
∴S△BOC=S△BOD+S△COD=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
∵直线x=t(t>0)与反比例函数y=
| 2 |
| x |
| 3 |
| x |
∴S△BOC=S△ABC=
| 5 |
| 2 |
故选:C.
点评:本题考查反比例函数系数k的几何意义,过双曲线上的任意一点分别向两条坐标轴作垂线,与坐标轴围成的矩形面积就等于|k|.本知识点是中考的重要考点,同学们应高度关注.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
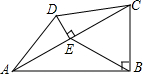 如图,在四边形ABCD中,∠ABC=90°,∠CAB=30°,DE⊥AC于E,且AE=CE,若DE=5,EB=12.求四边形ABCD的面积和∠DAC的正弦值.
如图,在四边形ABCD中,∠ABC=90°,∠CAB=30°,DE⊥AC于E,且AE=CE,若DE=5,EB=12.求四边形ABCD的面积和∠DAC的正弦值. 如图,△ABC中,∠B=∠C=70°,BP=CE,BD=CP,求∠DPE的度数.
如图,△ABC中,∠B=∠C=70°,BP=CE,BD=CP,求∠DPE的度数. 如图,在直角坐标系中,点A在x轴负半轴上,点B在x轴正半轴上,以线段AB为弦的⊙C与直线x=-2相切于点E(-2,
如图,在直角坐标系中,点A在x轴负半轴上,点B在x轴正半轴上,以线段AB为弦的⊙C与直线x=-2相切于点E(-2,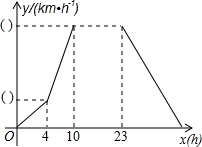 某气象研究中心观测一场沙尘暴从发生到结束的全过程.开始时风速平均每小时增加2km,4h后,沙尘暴经过开阔荒漠地,风速变为平均增加4km/h.一段时间,风速保持不变.当沙尘暴遇到绿色植被区时,其风速平均减小lkm/h,最终停止.结合风速y与时间x的图象(如图),回答下列问题.
某气象研究中心观测一场沙尘暴从发生到结束的全过程.开始时风速平均每小时增加2km,4h后,沙尘暴经过开阔荒漠地,风速变为平均增加4km/h.一段时间,风速保持不变.当沙尘暴遇到绿色植被区时,其风速平均减小lkm/h,最终停止.结合风速y与时间x的图象(如图),回答下列问题.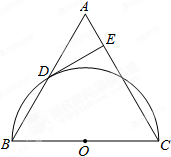 已知:如图,在△ABC中,AB=AC,以BC为直径的半圆O与边AB相交于点D,切线DE⊥AC,垂足为点E.求证:
已知:如图,在△ABC中,AB=AC,以BC为直径的半圆O与边AB相交于点D,切线DE⊥AC,垂足为点E.求证: 如图,在锐角△ABC中,CD、BE分别是AB、AC边上的高,且CD、BE相交于点P,若∠A=50°,则∠BPC=
如图,在锐角△ABC中,CD、BE分别是AB、AC边上的高,且CD、BE相交于点P,若∠A=50°,则∠BPC=