题目内容
 如图,在正方形网格中,△ABC各顶点都在格点上,点A,C的坐标分别为(-5,1)、(-1,4),结合所给的平面直角坐标系解答下列问题:
如图,在正方形网格中,△ABC各顶点都在格点上,点A,C的坐标分别为(-5,1)、(-1,4),结合所给的平面直角坐标系解答下列问题:(1)画出△ABC关于y轴对称的△A1B1C1;
(2)画出△A1B1C1关于x轴对称的△A2B2C2;
(3)点C1的坐标是
考点:作图-轴对称变换
专题:作图题
分析:(1)根据网格结构找出点A、B、C关于y轴的对称点A1、B1、C1的位置,然后顺次连接即可;
(2)根据网格结构找出点A1、B1、C1关于x轴的对称点A2、B2、C2的位置,然后顺次连接即可;
(3)根据平面直角坐标系写出点C1的坐标,利用勾股定理列式求出CC2,再根据三角形的周长的定义列式计算即可得解;利用△ABC所在的矩形的面积减去四周三个小直角三角形的面积列式计算即可得解.
(2)根据网格结构找出点A1、B1、C1关于x轴的对称点A2、B2、C2的位置,然后顺次连接即可;
(3)根据平面直角坐标系写出点C1的坐标,利用勾股定理列式求出CC2,再根据三角形的周长的定义列式计算即可得解;利用△ABC所在的矩形的面积减去四周三个小直角三角形的面积列式计算即可得解.
解答: 解:(1)△A1B1C1如图所示;
解:(1)△A1B1C1如图所示;
(2)△A2B2C2如图所示;
(3)C1(1,2),
由勾股定理得,CC2=
=2
,
所以,以C、C1、C2三点为顶点的三角形的周长=2+4+2
=6+2
,
S△ABC=3×4-
×2×4-
×3×1-
×1×3
=12-4-1.5-1.5
=12-7
=5.
故答案为:(1,2);6+2
;5.
 解:(1)△A1B1C1如图所示;
解:(1)△A1B1C1如图所示;(2)△A2B2C2如图所示;
(3)C1(1,2),
由勾股定理得,CC2=
| 22+42 |
| 5 |
所以,以C、C1、C2三点为顶点的三角形的周长=2+4+2
| 5 |
| 5 |
S△ABC=3×4-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=12-4-1.5-1.5
=12-7
=5.
故答案为:(1,2);6+2
| 5 |
点评:本题考查了利用轴对称变换作图,三角形的面积,熟练掌握网格结构准确找出对应点的位置是解题的关键.

练习册系列答案
相关题目
在下列各数:0.51525254…、
、
、
、
、
中,无理数的个数是( )
|
| 1 |
| π |
| 7 |
| 131 |
| 11 |
| 3 | 27 |
| A、2 | B、3 | C、4 | D、5 |
七棱柱的面数、顶点数、棱数分别是( )
| A、9,14,18 |
| B、7,14,21 |
| C、9、14、21 |
| D、7、14、21 |
 如图,△ABC中,∠B=∠C=70°,BP=CE,BD=CP,求∠DPE的度数.
如图,△ABC中,∠B=∠C=70°,BP=CE,BD=CP,求∠DPE的度数.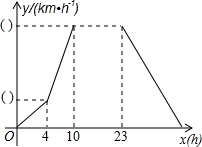 某气象研究中心观测一场沙尘暴从发生到结束的全过程.开始时风速平均每小时增加2km,4h后,沙尘暴经过开阔荒漠地,风速变为平均增加4km/h.一段时间,风速保持不变.当沙尘暴遇到绿色植被区时,其风速平均减小lkm/h,最终停止.结合风速y与时间x的图象(如图),回答下列问题.
某气象研究中心观测一场沙尘暴从发生到结束的全过程.开始时风速平均每小时增加2km,4h后,沙尘暴经过开阔荒漠地,风速变为平均增加4km/h.一段时间,风速保持不变.当沙尘暴遇到绿色植被区时,其风速平均减小lkm/h,最终停止.结合风速y与时间x的图象(如图),回答下列问题. 如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,点B为劣弧AN的中点.点P是直径MN上一动点,求PA+PB的最小值.
如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,点B为劣弧AN的中点.点P是直径MN上一动点,求PA+PB的最小值.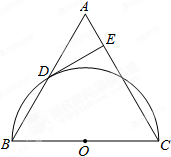 已知:如图,在△ABC中,AB=AC,以BC为直径的半圆O与边AB相交于点D,切线DE⊥AC,垂足为点E.求证:
已知:如图,在△ABC中,AB=AC,以BC为直径的半圆O与边AB相交于点D,切线DE⊥AC,垂足为点E.求证: 如图,已知∠B=∠C,AD=AE,求证:AB=AC.
如图,已知∠B=∠C,AD=AE,求证:AB=AC.