题目内容
2.阅读材料:求1+2+22+23+24+…+22015+22016的值.解:设 S=1+2+22+23+24+…+22015+22016,①
将①×2得:2S=2+22+23+24+…+22016+22017,②
由 ②-①得:2S-S=22017-1,即S=22017-1,
即1+2+22+23+24+…+22015+22016=22017-1
请你仿照此法计算:1+3+32+33+34+…+3n(其中n为正整数).
分析 仿照例子,设S=1+3+32+33+34+…+3n,由此可得出3S=3+32+33+34+…+3n+1,两者做差即可得出3S-S=3n+1-1,由此即可得出结论.
解答 解:设S=1+3+32+33+34+…+3n①(其中n为正整数),
将①×3得:3S=3+32+33+34+…+3n+1②,
由②-①得:3S-S=3n+1-1,即S=$\frac{{3}^{n+1}-1}{2}$,
故1+3+32+33+34+…+3n=$\frac{{3}^{n+1}-1}{2}$(其中n为正整数).
点评 本题考查了规律型中的数字的变化类,解题的关键是仿照例子计算1+3+32+33+…+3n.本题属于基础题,难度不大,本题其实是等比数列的求和公式,但初中未接触过该方面的知识,需要借助于错位相减法来求出结论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.对于实数a、b,定义一种新运算“?”为:a?b=$\frac{1}{{a-{b^2}}}$,这里等式右边是实数运算.例如:1?3=$\frac{1}{{1-{3^2}}}=-\frac{1}{8}$.则方程x?(-2)=$\frac{2}{x-4}$-1的解是( )
| A. | x=4 | B. | x=5 | C. | x=6 | D. | x=7 |
13.计算2016×2012-20142的结果是( )
| A. | 1 | B. | -1 | C. | -4 | D. | 4 |
10.方程3x+y=9在正整数范围内的解的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 有无数个 |
17.若x使(x-1)2=4成立,则x的值是( )
| A. | 3 | B. | -1 | C. | 3或-1 | D. | ±2 |
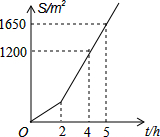 明君社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率.该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是( )
明君社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率.该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是( )